ML approach
Under certain conditions, the J-function is independent of 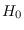 as long
as
as long
as 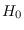 remains within the “region of sufficiency" (ROS) for
remains within the “region of sufficiency" (ROS) for  (See Section 2.3.3).
Then,
(See Section 2.3.3).
Then, 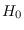 can even “float" with the data
as long as it remains in the ROS.
The ROS can be spanned by a parametric model
can even “float" with the data
as long as it remains in the ROS.
The ROS can be spanned by a parametric model
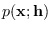 as long as (a)
as long as (a)
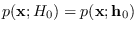 for some parameter
for some parameter 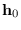 , and (b)
, and (b)
 is a sufficient statistic for
is a sufficient statistic for 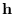 .
.
We can easily meet these conditions using
the multi-variate TED distribution (7.5) with
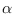
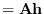 .
Condition (a) is met by
.
Condition (a) is met by
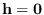 . Condition (b)
is met since (7.5) can be written
. Condition (b)
is met since (7.5) can be written
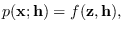 for some function
for some function 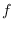 . It therefore follows that
. It therefore follows that
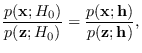 |
(17.16) |
for any 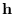 , where
, where
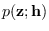 is defined as the
distribution of
is defined as the
distribution of  when
when
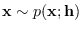 .
Since the ratio (17.16) does not depend on
.
Since the ratio (17.16) does not depend on
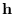 , it makes sense to place
, it makes sense to place 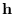 at the
point where
at the
point where
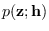 can be easily evaluated,
and that is the point where both
can be easily evaluated,
and that is the point where both
 and
and
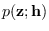 have their maximum value, that is to say
at the maximum likelihood (ML) point
have their maximum value, that is to say
at the maximum likelihood (ML) point
At this point, we can apply the central limit theorem
to find
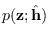 . The mean is given by
. The mean is given by
where
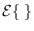 is expected value,
and
is expected value,
and
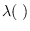 is the TED mean (7.3).
Note that under
is the TED mean (7.3).
Note that under
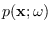 ,
,
where
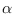
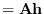 [97,98].
From this, we can solve for the variance of
[97,98].
From this, we can solve for the variance of 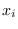 ,
,
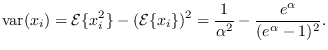 |
(17.17) |
The covariance of  is therefore
is therefore
where  is the diagonal matrix with elements (17.17).
Finally, then, we apply (17.16) at
is the diagonal matrix with elements (17.17).
Finally, then, we apply (17.16) at
 ,
and
,
and
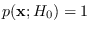 , to get
, to get
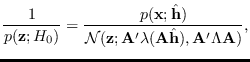 |
(17.18) |
where
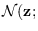
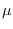
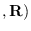 is the Gaussian distribution
with mean
is the Gaussian distribution
with mean
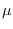 and covariance
and covariance 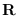 .
This approach can then be compared numerically with the
reciprocal of (2.12).
.
This approach can then be compared numerically with the
reciprocal of (2.12).
![]()
![]() .
Condition (a) is met by
.
Condition (a) is met by
![]() . Condition (b)
is met since (7.5) can be written
. Condition (b)
is met since (7.5) can be written
![]() for some function
for some function ![]() . It therefore follows that
. It therefore follows that
![$\displaystyle {\cal E}\{x_i^2\} =
\frac{2}{\alpha^2}
\left[
\frac{1-\frac{1}{2} \left( \alpha^2 -2\alpha + 2\right) e^\alpha}{1-e^\alpha}
\right],$](img1966.png)