We now compare the methods of Sections 17.7.1 and 17.7.2
for a special case where
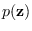 can be computed exactly.
Consider the trivial case where
can be computed exactly.
Consider the trivial case where
![${\bf A}=[1, \; 1, \ldots 1]^\prime$](img1974.png) .
In this case
.
In this case
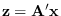 has the Irwin-Hall distribution
has the Irwin-Hall distribution
where
 In Figure 17.1, we show the
In Figure 17.1, we show the
 error (compared with exact Irwin-Hall distribution)
on the Y-axis for both methods for
error (compared with exact Irwin-Hall distribution)
on the Y-axis for both methods for 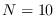 and
and 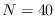 .
The error is very small, less that .02 at
.
The error is very small, less that .02 at 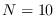 and less than .004 at
and less than .004 at 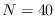 .
This error for a 40-dimensional PDF is very small
and for all practical purposes, can be ignored.
Notice that the error becomes smaller with increasing
.
This error for a 40-dimensional PDF is very small
and for all practical purposes, can be ignored.
Notice that the error becomes smaller with increasing  .
For even larger
.
For even larger  , however, the round-off error in computing Irwin-Hall
eventually dominates.
Although almost always the same, the ML approach had slightly more
error and the SPA was faster. Therefore, SPA is our method of choice.
, however, the round-off error in computing Irwin-Hall
eventually dominates.
Although almost always the same, the ML approach had slightly more
error and the SPA was faster. Therefore, SPA is our method of choice.
Figure:
Numerical comparison of SPA (dots) and
ML (circles) with Irwin-Hall distribution (X-axis)
for 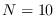 and
and 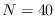 .
.
|
|
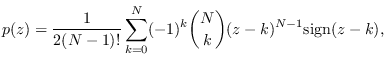
![\includegraphics[width=5.4in]{irwinhall.eps}](img1977.png)