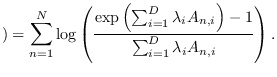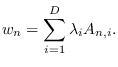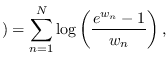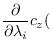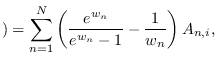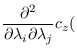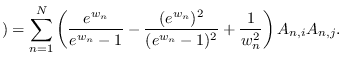Saddlepoint Approximation for Linear Function of Uniformly-Distributed Data
We follow the method of Section 2.3.2.
Let  be a set of
be a set of 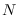 independent uniform-distributed RV in
independent uniform-distributed RV in ![$[0,1]$](img9.png) Let
Let 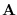 be an
be an 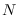 -by-
-by-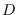 full-rank matrix and let
full-rank matrix and let
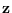 be the
be the 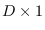 feature vector
feature vector
When
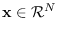 is uniformly distributed, the CGF is given by
is uniformly distributed, the CGF is given by
For conciseness, define
Then,
and
From these expressions, we may find the saddle-point (2.12).
![]() is uniformly distributed, the CGF is given by
is uniformly distributed, the CGF is given by