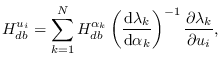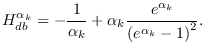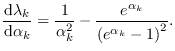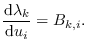Solving for asymptotic mean of MCMC-UMS
We can apply the method of section 5.3.2 approximate the
asymptotic mean of MCMC-UMS for doubly-bounded data.
In other words, we propose to model
the distribution of MCMC-UMS generated
data by (7.6).
We then maximize the entropy of this distribution
over the mean under the constraint that the mean
is on the manifold. More precisely,
we propose to maximize the entropy of (7.6)
over
 subject to (5.12).
Unfortunately, the entropy is written in terms of
both
subject to (5.12).
Unfortunately, the entropy is written in terms of
both
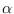 and
and
 . But, it can be shown
that for a given
. But, it can be shown
that for a given  , there is a unique
, there is a unique
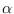 [49].
This is true in one or more dimensions. Therefore,
[49].
This is true in one or more dimensions. Therefore,
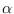 and
and
 are alternative parameterizations for
the multivariate truncated exponential distribution.
are alternative parameterizations for
the multivariate truncated exponential distribution.
In the same manner as in Sections 4.4 and 5,
we use 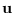 as the free variable
under the constraint (5.12).
So, to maximize (7.6), we need
the derivatives of (7.6)
with respect to the elements of
as the free variable
under the constraint (5.12).
So, to maximize (7.6), we need
the derivatives of (7.6)
with respect to the elements of 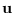 .
Using the derivative chain-rule, we can write the first
derivative of (7.6) with respect to
.
Using the derivative chain-rule, we can write the first
derivative of (7.6) with respect to 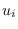
where, from (7.6)
From (7.3) ,
And, from (5.10),
After (a lot of) cancellations, we get
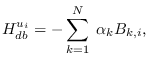 |
(7.7) |
resulting in the condition for maximization of entropy:
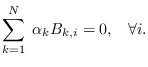 |
(7.8) |
Subsections
![]() as the free variable
under the constraint (5.12).
So, to maximize (7.6), we need
the derivatives of (7.6)
with respect to the elements of
as the free variable
under the constraint (5.12).
So, to maximize (7.6), we need
the derivatives of (7.6)
with respect to the elements of ![]() .
Using the derivative chain-rule, we can write the first
derivative of (7.6) with respect to
.
Using the derivative chain-rule, we can write the first
derivative of (7.6) with respect to ![]()