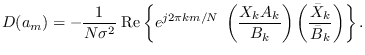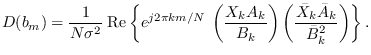CR Bound analysis of the exact PDF of an ARMA processes - filtering approach.
The results of section 10.2.6 are still a little bit cumbersome to
implement.
Using filtering, we may find a much more efficient approach to finding the
derivatives of the exact ARMA PDF (10.6).
We can rewrite (10.27) as
In the time domain, this suggests a correlation between u and v where
u = filter(a,b,x)/sqrt(sig2);
v = filter(1,b,x)/sqrt(sig2);
for m=1:P,
da(m)= -sum(u(K+1:N) .* v(K+1-m:N-m));
end;
where 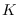 is the impulse response length of the
wihtening filter (Section 10.2.3).
Similarly, we can rewrite (10.28) as
is the impulse response length of the
wihtening filter (Section 10.2.3).
Similarly, we can rewrite (10.28) as
In the time domain, this suggests a correlation between u and w, where
u = filter(a,b,x)/sqrt(sig2);
w=filter(1,b,u);
for m=1:Q,
db(m)= sum(u(K+1:N) .* w(K+1-m:N-m));
end;
Of course, this approach, however, misses the first 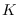 elements in the summation.
In fact, we can patch it up.
If we use Section 10.2.2 for the first
elements in the summation.
In fact, we can patch it up.
If we use Section 10.2.2 for the first 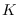 elements only,
then add in the above values, we can obtain an exact hybrid approach based on filtering
with order
elements only,
then add in the above values, we can obtain an exact hybrid approach based on filtering
with order  computation. See software/pdf_arma_exact.m.
computation. See software/pdf_arma_exact.m.