Exact PDF of an ARMA process - Efficient method using Levinson algorithm
The exact PDF of an ARMA process can be written as in (10.6)
where 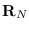 is the symmetric Toeplitz
is the symmetric Toeplitz
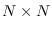 covariance matrix of an ARMA process
formed from (10.15).
Computing
covariance matrix of an ARMA process
formed from (10.15).
Computing 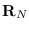 , and even just storing it, for large
, and even just storing it, for large  is inefficient.
Using the Levinson algorithm, an efficient implementation of the exact PDF may be obtained.
is inefficient.
Using the Levinson algorithm, an efficient implementation of the exact PDF may be obtained.
When  is large, the computing the term
is large, the computing the term
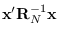 is prohibitive
and when
is prohibitive
and when  is very large, even storing
is very large, even storing 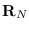 is inefficient.
The problem is solved efficiently using the Levinson algorithm.
Let x be an N-by-1 vector and let
is inefficient.
The problem is solved efficiently using the Levinson algorithm.
Let x be an N-by-1 vector and let 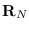 be the symmetric N-by-N Toeplitz matrix
formed from the N-by-1 ACF vector r. The function
be the symmetric N-by-N Toeplitz matrix
formed from the N-by-1 ACF vector r. The function
[y,ldetR] = toepsolve(r,x,N);
is the same as
R = toeplitz(r(1:N));
y = R \ x;
ldetR = log(det(R));
We then have
The execution time of
software/toepsolve.m is much faster (see Figure 10.3)
and includes as a by-product the determinant of R.
As predicted by theory, the standard approach is order 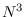 , while Levinson is
, while Levinson is 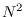 .
.
Figure 10.3:
Comparison of execution times of y = R b versus y = toepsolve(r,b,N) as
a function of N.
|
|
The exact PDF can be therefore computed by
[y,ldetR] = toepsolve(r,x,N);
lpx = -N/2*log(2*pi) -.5*ldetR -.5*x'*y;
![]() is large, the computing the term
is large, the computing the term
![]() is prohibitive
and when
is prohibitive
and when ![]() is very large, even storing
is very large, even storing ![]() is inefficient.
The problem is solved efficiently using the Levinson algorithm.
Let x be an N-by-1 vector and let
is inefficient.
The problem is solved efficiently using the Levinson algorithm.
Let x be an N-by-1 vector and let ![]() be the symmetric N-by-N Toeplitz matrix
formed from the N-by-1 ACF vector r. The function
be the symmetric N-by-N Toeplitz matrix
formed from the N-by-1 ACF vector r. The function
![\includegraphics[width=4.5in,height=3.0in, clip]{arma_exact_times.eps}](img1115.png)