If the roots of the denominator polynomial are inside the unit circle,
the ACF of the ARMA process, 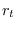 , will go to zero for
, will go to zero for 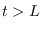 for some
for some 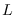 .
Let
.
Let 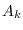 and
and 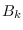 be the DFT of
be the DFT of 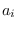 and
and 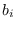 padded to length
padded to length 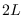 .
Then the circular power spectrum of size
.
Then the circular power spectrum of size 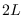 is
is
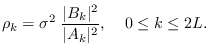 |
(10.14) |
Then,
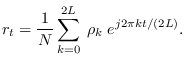 |
(10.15) |
The first 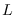 values of
values of 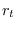 will be accurate approximations to the true ACF.
In MATLAB:
will be accurate approximations to the true ACF.
In MATLAB:
A=fft([a(:); zeros(2*L-P-1,1)]);
B=fft([b(:); zeros(2*L-Q-1,1)]);
A2=msq(A);
B2=msq(B);
h = B2./A2;
rho = sig2 * h;
r = real(ifft(rho));
One only needs to increase 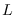 until the condition is met that
the ACF dies to zero before
until the condition is met that
the ACF dies to zero before 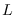 . See figure 10.2.
. See figure 10.2.
Figure:
Computing ACF with the DFT. Upper panel,  too small.
Lower panel
too small.
Lower panel  large enough.
large enough.
|
|