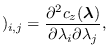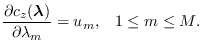SPA Solution for Order Statistics of Exponential RVs (module_exp_ord.m)
We derive a multidimensional Saddlepoint solution
as an alternative to (8.4).
We consider only the first case (exponential RVs).
This will provide a means of validating the
integral solution of the previous section.
Let
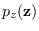 be a PDF defined on the space
be a PDF defined on the space
 .
The saddlepoint approximation is given by [16]
.
The saddlepoint approximation is given by [16]
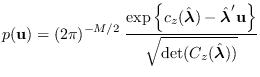 |
(8.7) |
where
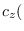

 is the joint cumulant
generating function (CGF)
is the joint cumulant
generating function (CGF)
and
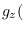

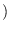 is the joint moment function of
is the joint moment function of
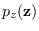 ,
and
,
and
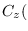

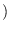 is the
is the 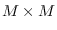 Hessian matrix
of
Hessian matrix
of
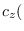

 :
:
and
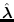 is the saddle point, the value of
is the saddle point, the value of
 where
where
Thus, to obtain the SPA, we need the joint CGF
and its first and second-order partial derivatives.
Subsections
![]() be a PDF defined on the space
be a PDF defined on the space
![]() .
The saddlepoint approximation is given by [16]
.
The saddlepoint approximation is given by [16]