We start with the joint MGF of 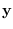 , which is (see [54],
p. 68, eq. B-18)
, which is (see [54],
p. 68, eq. B-18)
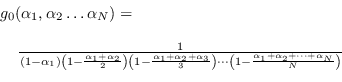 |
(8.8) |
for
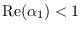 ,
,
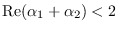 ,
... ,
,
... ,
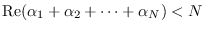 .
We can rewrite (8.8) as
.
We can rewrite (8.8) as
where
Alternatively,
where
Define the 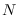 -by-
-by-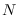 matrix
matrix
![${\bf Q}=[q_{np}]$](img862.png) and
and
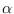
![$=[\alpha_1\;\alpha_2 \cdots \alpha_N]^\prime$](img863.png) .
Then,
.
Then,
where
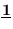 is an
is an 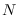 -by-1
column vector of ones.
Thus,
-by-1
column vector of ones.
Thus,
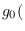
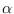
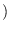 is the reciprocal
of the product of the elements of
is the reciprocal
of the product of the elements of
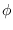
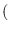
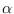
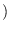 ,
denoted by
,
denoted by
where
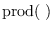 is the product of the
elements of the argument.
is the product of the
elements of the argument.
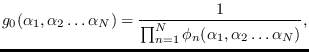
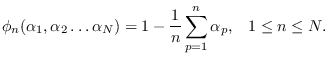
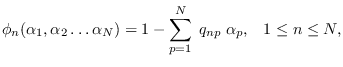
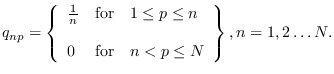
![$\displaystyle ) \stackrel{\mbox{\tiny$\Delta$}}{=}
\left[ \begin{array}{c}
\p...
...
\end{array}\right] =
{\underline{\bf 1}}- {\bf Q} \mbox{\boldmath$\alpha$},
$](img865.png)