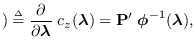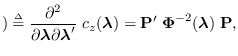To obtain the SPA to the PDF of  , we need
the joint cumulant generating function (CGF)
, we need
the joint cumulant generating function (CGF)
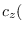
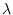
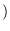 of
of  and its partial derivatives. The joint CGF is defined by
and its partial derivatives. The joint CGF is defined by
where
log is the vector  function
which operates on each element of its argument and
function
which operates on each element of its argument and
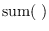 is the vector sum,
which adds up all the elements of the argument.
If we define
is the vector sum,
which adds up all the elements of the argument.
If we define
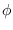
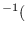
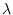
 as the element-by-element
reciprocal of
as the element-by-element
reciprocal of
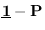
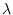 ,
and
,
and
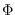
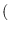
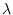
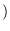 as the diagonal
as the diagonal
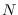 -by-
-by-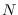 matrix with elements
equal to the elements of
matrix with elements
equal to the elements of
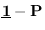
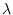 ,
it is straight-forward to show that the gradient vector
of
,
it is straight-forward to show that the gradient vector
of
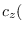
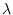
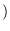 is the
is the 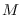 -by-1 vector
-by-1 vector
and the 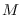 -by-
-by-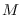 Hessian matrix of
Hessian matrix of
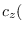
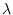
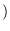 is
is