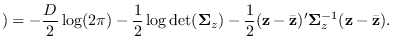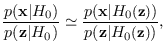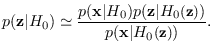General solution using CLT (module_A_chisq_clt.m)
The SPA is the preferred solution to solve
for
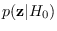 , but for completeness,
and to serve as a comparison of the SPA approach, we cover the CLT solution.
Because we intend to use the CLT to approximate
, but for completeness,
and to serve as a comparison of the SPA approach, we cover the CLT solution.
Because we intend to use the CLT to approximate
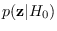 , we need to use a floating reference hypothesis,
(See Sections 2.3.3 and 2.3.4)
, we need to use a floating reference hypothesis,
(See Sections 2.3.3 and 2.3.4)
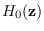 and corresponding J-function
and corresponding J-function
We seek a
 such that the mean of
such that the mean of 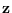 under
under
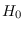
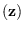 is
equal to or close to the given feature value, which we
designate
is
equal to or close to the given feature value, which we
designate 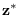 .
There are two possible methods. For arbitrary
matrices
.
There are two possible methods. For arbitrary
matrices 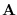 , this can be done by projecting the input vector
upon the column space of
, this can be done by projecting the input vector
upon the column space of 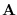 ,
,
or
This will satisfy the constraint
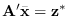 ,
however may be invalid if it has negative values.
,
however may be invalid if it has negative values.
The problem of negative values can be solved
by finding a suitable positive-valued approximation,
using quadratic programming to
find the positive-valued (non-zero)
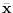 that minimizes
that minimizes
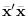 under the constraint that
under the constraint that
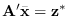 .
For example MATLAB optimization toolkit has quadprog.m which
solves the above problem with the syntax
.
For example MATLAB optimization toolkit has quadprog.m which
solves the above problem with the syntax
x = quadprog(eye(N),zeros(N,1),[],[],A',z,meps*ones(N,1));
where meps is a small positive number (minimum allowed value of 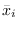 ).
A good
).
A good
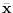 also results if we minimize the spectral entropy
also results if we minimize the spectral entropy
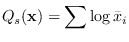 |
(5.5) |
under the same constraints.
Another particularly elegant solution to find
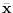 can be found in time-series analysis
where we use the autoregressive spectrum estimate for
can be found in time-series analysis
where we use the autoregressive spectrum estimate for
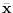 .
We will discuss this in section 5.2.5.
.
We will discuss this in section 5.2.5.
Regardless of which method we used to obtain
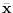 ,
let
,
let
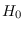
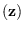 be the hypothesis that
be the hypothesis that  has mean
has mean
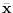 ,
with
,
with
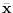 satisfying (or nearly satisfying)
the constraint
satisfying (or nearly satisfying)
the constraint
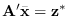 .
Therefore, under
.
Therefore, under
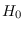
 , the mean of
, the mean of 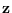 is near to
is near to 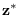 itself.
In section 2.3.3, we discussed the concept of the region of sufficiency (ROS).
itself.
In section 2.3.3, we discussed the concept of the region of sufficiency (ROS).
When applying the central limit theorem, we need only consider the mean
and variance of 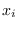 . For the
chi-squared RV, the mean is
. For the
chi-squared RV, the mean is 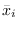 and the variance
is
and the variance
is
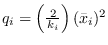 .
The mean of
.
The mean of 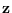 is therefore
is therefore
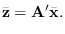
The covariance of 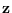 under
under
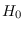
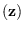 is
is
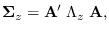
where 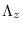 is the diagonal matrix with diagonal elements
is the diagonal matrix with diagonal elements
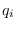 . We can immediately write down the J-function denominator,
. We can immediately write down the J-function denominator,
If
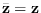 , then the last term disappears.
, then the last term disappears.
Example 9
We now re-examine example 8, however this time we
apply the CLT method.
Once again, projected PDF values are plotted against the true values of
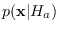 in Figure 5.3.
The acid test passes.
The function software/module_A_chisq implements reature trasformation and J-function.
The function software/module_A_chisq_test.m runs the acid test
(with variable CLT set to 1) using syntax:
in Figure 5.3.
The acid test passes.
The function software/module_A_chisq implements reature trasformation and J-function.
The function software/module_A_chisq_test.m runs the acid test
(with variable CLT set to 1) using syntax:
module_A_chisq_test('acid',100,2,2,”,1);
It is interesting to compare
the Jout values from the SPA and CLT methods.
In Figure 5.4, we see there is close agreement.
Mathematically, we have
where the right hand side is the J-function from the CLT method using
the floating reference hypothesis. Clearly then,
Note that this provides an alternative to the SPA
for computing the PDF of
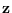 under a fixed reference hypothesis.
under a fixed reference hypothesis.
Figure 5.3:
Acid test results for module_A_chisq_clt.m.
|
|
Figure 5.4:
Jout comparison for SPA and CLT.
|
|
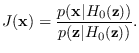
![]() that minimizes
that minimizes
![]() under the constraint that
under the constraint that
![]() .
For example MATLAB optimization toolkit has quadprog.m which
solves the above problem with the syntax
.
For example MATLAB optimization toolkit has quadprog.m which
solves the above problem with the syntax
![]() can be found in time-series analysis
where we use the autoregressive spectrum estimate for
can be found in time-series analysis
where we use the autoregressive spectrum estimate for
![]() .
We will discuss this in section 5.2.5.
.
We will discuss this in section 5.2.5.
![]() ,
let
,
let
![]()
![]() be the hypothesis that
be the hypothesis that ![]() has mean
has mean
![]() ,
with
,
with
![]() satisfying (or nearly satisfying)
the constraint
satisfying (or nearly satisfying)
the constraint
![]() .
Therefore, under
.
Therefore, under
![]()
![]() , the mean of
, the mean of ![]() is near to
is near to ![]() itself.
In section 2.3.3, we discussed the concept of the region of sufficiency (ROS).
itself.
In section 2.3.3, we discussed the concept of the region of sufficiency (ROS).
![]() . For the
chi-squared RV, the mean is
. For the
chi-squared RV, the mean is ![]() and the variance
is
and the variance
is
![]() .
The mean of
.
The mean of ![]() is therefore
is therefore