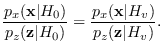Data Normalization
An application of the floating reference hypothesis is
normalization of data prior to evaluation of the SPA for
a fixed reference hypothesis.
Suppose we would like to evaluate
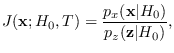 |
(2.16) |
for arbitrary vectors  .
Let
.
Let  be an estimate of the scale of
be an estimate of the scale of  , either
a sample variance, sample mean, or standard deviation estimate.
Important is that as
, either
a sample variance, sample mean, or standard deviation estimate.
Important is that as  is scaled, all the elements of
is scaled, all the elements of  will vary in proportion to
will vary in proportion to  :
:
Let 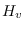 be a reference hypothesis that depends on
be a reference hypothesis that depends on 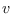 .
As long as the feature
.
As long as the feature  contains
contains 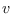 , or
, or 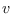 can be computed
from
can be computed
from  , then
, then 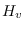 remains in the ROS of
remains in the ROS of  . Thus,
equation (2.13) is theoretically independent of
. Thus,
equation (2.13) is theoretically independent of 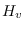 ,
,
If the elements of  are linearly related to
are linearly related to 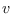 ,
we may write
,
we may write
where 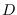 is the dimension of
is the dimension of  .
Therefore,
.
Therefore,
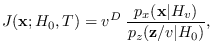 |
(2.17) |
which provides a convenient way to normalize  prior to calculating the SPA.
prior to calculating the SPA.
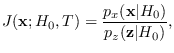
![]() be a reference hypothesis that depends on
be a reference hypothesis that depends on ![]() .
As long as the feature
.
As long as the feature ![]() contains
contains ![]() , or
, or ![]() can be computed
from
can be computed
from ![]() , then
, then ![]() remains in the ROS of
remains in the ROS of ![]() . Thus,
equation (2.13) is theoretically independent of
. Thus,
equation (2.13) is theoretically independent of ![]() ,
,