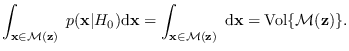Next: PDF Projection validation: the Up: Implementation Previous: Maximum Likelihood Modules Contents
Another interpretation, based on asymptotic
maximum likelihood (ML) theory, starts by
assuming that there exists some parametric model
![]()
![]()
![]() such that the features are
maximum likelihood estimates of the parameters,
such that the features are
maximum likelihood estimates of the parameters,
![]() .
The J-function for ML, given in (2.27), is dominated by
the numerator, which is the likelihood function of the data
evaluated at
.
The J-function for ML, given in (2.27), is dominated by
the numerator, which is the likelihood function of the data
evaluated at
![]() .
Thus, the J-function has the interpretation as
a quantitative measure of how well the parametric
model can describe the raw data. The better the features, the better this
notional parametric model. Interestingly, because the J-function
can be computed without
actually implementing the ML estimator, this information
is available without needing to know the parametric form nor
needing to maximize it!
Naturally, there are situations where this information
is detrimental to classification - specifically if the data contains
nuisance information or interference.
There are work-arounds that significantly
improve classification performance, for example the
class-specific feature mixture ([20], section II.B).
.
Thus, the J-function has the interpretation as
a quantitative measure of how well the parametric
model can describe the raw data. The better the features, the better this
notional parametric model. Interestingly, because the J-function
can be computed without
actually implementing the ML estimator, this information
is available without needing to know the parametric form nor
needing to maximize it!
Naturally, there are situations where this information
is detrimental to classification - specifically if the data contains
nuisance information or interference.
There are work-arounds that significantly
improve classification performance, for example the
class-specific feature mixture ([20], section II.B).
There is also a geometric interpretation that lends insight
into the general approach. For the uniform reference
hypothesis (
![]() ),
(2.2) reduces to
),
(2.2) reduces to
![]() ,
but
,
but
![]() is just the volume of the manifold (2.4):
is just the volume of the manifold (2.4):