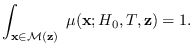Generation of Samples from
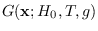
Indeed,
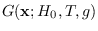 is a generative model.
In this book, we will continually discuss
the generative process of creating synthetic samples of
is a generative model.
In this book, we will continually discuss
the generative process of creating synthetic samples of
 by drawing samples from
by drawing samples from
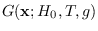 .
Generation of data from
.
Generation of data from
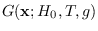 is accomplished
using the following process ([3], Section 2.1)
is accomplished
using the following process ([3], Section 2.1)
- Draw a sample
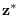 from
from
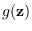 ,
,
- Determine the manifold
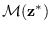 ,
which is the set of all points
,
which is the set of all points
 that map to
that map to 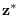 through transformation
through transformation
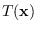 :
:
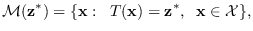 |
(2.4) |
where 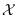 is the set of valid input data samples
is the set of valid input data samples
 .
It is common to call
.
It is common to call
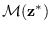 a manifold or level set
2.2.
a manifold or level set
2.2.
- draw a sample
 from
from
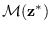 according to a distribution
proportional to
according to a distribution
proportional to
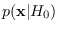 .
.
Note that drawing a sample  from
from
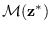 according to a distribution
proportional to
according to a distribution
proportional to
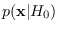 can be regarded as a a posteriori
distribution of
can be regarded as a a posteriori
distribution of  given
given  . But, it is not a proper
distribution since all its probability mass exists on
. But, it is not a proper
distribution since all its probability mass exists on
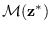 which has zero volume, and so must have infinite value.
If we restrict our analysis just to the set
which has zero volume, and so must have infinite value.
If we restrict our analysis just to the set
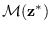 , we can
write down a representative distribution, called
the manifold distribution
, we can
write down a representative distribution, called
the manifold distribution
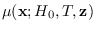 ,
,
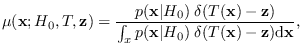 |
(2.5) |
where
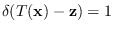 when
when
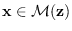 and is zero
otherwise. Clearly
and is zero
otherwise. Clearly
Intuitively, the manifold distribution is just a distribution
on
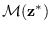 that is proportional to
that is proportional to
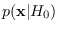 .
.
Subsections