Maximum Likelihood Modules

A special case of the floating reference hypothesis approach is the maximum likelihood (ML) method, when 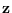${\bf z}$ is an (ML) estimator (See section 2.3.5)

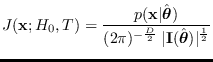$$J({\bf x};H_0,T) = {p({\bf x}\vert\hat{\mbox{\boldmath$\theta$}})... ...ac{D}{2}} \; \vert{\bf I}( \hat{\mbox{\boldmath$\theta$}})\vert^{\frac{1}{2}} }$$ (2.27)

To continue the example above, it is known that the ML estimator for variance is the sample variance which has a Cramer-Rao (CR) bound of 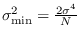$\sigma^2_{\rm min}=\frac{2\sigma^4}{N}$. Applying (2.20), we get exactly the same result as the above floating reference approach. Whenever the feature is also a ML estimate and the asymptotic results apply (the number of estimated parameters is small and the amount of data is large), the two methods are identical. The floating reference hypothesis method is more general because it does not need to rely on the CLT and there does not need to be a floating reference hypothesis parameter corresponding to each features, as in the ML method.