Figure 12.1 shows a generalized representation
of block segmentation for PDF projection-based
models. The input data  is segmented in various ways. In the figure
is segmented in various ways. In the figure
 is divided into 1, 2, 3, and 4 equal
segments. In general, the segments do not need to be
of uniform size.
What distiguishes block segmentation from other types
is the fact that the segments are non-overlapping
and no window function is used (rectangular weighting).
It is also important that all samples of
is divided into 1, 2, 3, and 4 equal
segments. In general, the segments do not need to be
of uniform size.
What distiguishes block segmentation from other types
is the fact that the segments are non-overlapping
and no window function is used (rectangular weighting).
It is also important that all samples of  are
included in the totality of the segments.
This means that for uniform-sized segments,
the input size
are
included in the totality of the segments.
This means that for uniform-sized segments,
the input size  must be an integer multiple
of the segment size. For this reason, it is prudent to truncate all
input data
must be an integer multiple
of the segment size. For this reason, it is prudent to truncate all
input data  to a multiple of some highly divisible
number, such as
to a multiple of some highly divisible
number, such as 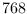 .
.
In Figure 12.1, each branch uses a different
uniform segment size, and the same feature transformation
is used for all segments in each branch.
The uniform segmentation and uniform feature
extraction is the most common because it lends
itself to PDF estimation using HMM (Section 13.3).
In general, the segmentation can be non-uniform and different
feature transformations can be used within a branch.
Furthermore, some branches could use the
same segmentation, but different feature transformations.
Figure:
Block-segmentation architecture. The same input data  is presented to each branch, where it may be differently
segmented, and processed by different feature extraction
transformations. The output of branch
is presented to each branch, where it may be differently
segmented, and processed by different feature extraction
transformations. The output of branch 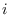 is the
projected PDF
is the
projected PDF
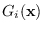 . The branch outputs are combined or compared.
. The branch outputs are combined or compared.
|
|
Block segmentation is necessary
for strict interpretation of the
PDF projection theorem in the presence
of segmented data.
Let's talk about one branch in Figure 12.1.
Let 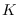 be the segment size, so
be the segment size, so 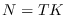 , where
, where
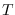 is the number of segments. Then,
is the number of segments. Then,
Let 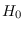 be the reference hypothesis, in which
the samples of
be the reference hypothesis, in which
the samples of  are iid, either exponential
(3.9) or Gaussian (3.11).
It follows that the segments are independent,
are iid, either exponential
(3.9) or Gaussian (3.11).
It follows that the segments are independent,
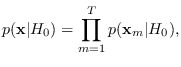 |
(12.1) |
and if each segment feature is computed from the
corresponding data segment,
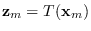 ,
we have
,
we have
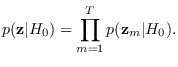 |
(12.2) |
Then, PDF projection (2.2) is applied
using (12.1) and (12.2).
The joint feature PDF
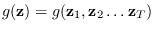 is obtained from the HMM forward procedure (Section 13.3).
Thus, block segmentation allows
the exact application of PDF projection (2.2)
through the strict independence of the segments under
is obtained from the HMM forward procedure (Section 13.3).
Thus, block segmentation allows
the exact application of PDF projection (2.2)
through the strict independence of the segments under 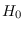 .
There are, however, significant disadvantages of block
segmentation.
It is not guaranteed that the segment boundaries fall at
appropriate times. The occurrences of events in the data
may get split into several segments, and extreme Gibbs-effect
will be seen in the frequency domain. The result can be
poor and erratic feature extraction.
For these reasons, it may be prefereable to use
overlapped/windowed segments.
.
There are, however, significant disadvantages of block
segmentation.
It is not guaranteed that the segment boundaries fall at
appropriate times. The occurrences of events in the data
may get split into several segments, and extreme Gibbs-effect
will be seen in the frequency domain. The result can be
poor and erratic feature extraction.
For these reasons, it may be prefereable to use
overlapped/windowed segments.
![\includegraphics[height=2.5in,width=5.5in]{topology.eps}](img1314.png)
![]() be the segment size, so
be the segment size, so ![]() , where
, where
![]() is the number of segments. Then,
is the number of segments. Then,