In order to proceed with PDF projection, we need to have a reference hypothesis,
which we have explained, provides a way of specifying
the distribution of the unobservable dimensions of  .
The reference hypothesis can be any statistical hypothesis under which the distribution
of both
.
The reference hypothesis can be any statistical hypothesis under which the distribution
of both  and
and  are known, and denoted by
the pair
are known, and denoted by
the pair
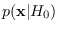 ,
,
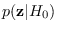 .
Usually,
.
Usually,
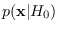 selected based on some general knowledge about the input data,
such as value range (i.e. is the data positive, is it constrained
to the interval [0, 1], is it unconstrained, but with a known variance).
Under these general constraints, we select the distribution with
highest entropy (see Chapter 3). This has a double benefit: selecting maximum entropy
reduces bias in the selection of
selected based on some general knowledge about the input data,
such as value range (i.e. is the data positive, is it constrained
to the interval [0, 1], is it unconstrained, but with a known variance).
Under these general constraints, we select the distribution with
highest entropy (see Chapter 3). This has a double benefit: selecting maximum entropy
reduces bias in the selection of
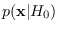 and
often results in a canonical distribution for which
and
often results in a canonical distribution for which
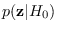 can be derived.
can be derived.
Note that 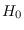 is a purely mathematical concept, and does not
need to represent any type of “noise-only" condition
or realistic data or such.
is a purely mathematical concept, and does not
need to represent any type of “noise-only" condition
or realistic data or such.
Other means of selecting
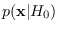 can be used.
First, in Section 2.2.2, we will discuss
how
can be used.
First, in Section 2.2.2, we will discuss
how 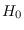 and
and
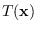 can be selected jointly
to approximate the condition of sufficiency, and thereby
approximate as close as possbile the distribution
of
can be selected jointly
to approximate the condition of sufficiency, and thereby
approximate as close as possbile the distribution
of  under some arbitrary hypothesis
under some arbitrary hypothesis 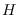 .
.
For now, let's just assume that 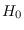 is given.
Normally,
is given.
Normally,
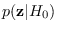 must be derived analytically.
Only in rare situations can
must be derived analytically.
Only in rare situations can
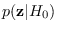 can be estimated.
We discuss type of problem in Section 2.2.3.
can be estimated.
We discuss type of problem in Section 2.2.3.
![]() is a purely mathematical concept, and does not
need to represent any type of “noise-only" condition
or realistic data or such.
is a purely mathematical concept, and does not
need to represent any type of “noise-only" condition
or realistic data or such.
![]() can be used.
First, in Section 2.2.2, we will discuss
how
can be used.
First, in Section 2.2.2, we will discuss
how ![]() and
and
![]() can be selected jointly
to approximate the condition of sufficiency, and thereby
approximate as close as possbile the distribution
of
can be selected jointly
to approximate the condition of sufficiency, and thereby
approximate as close as possbile the distribution
of ![]() under some arbitrary hypothesis
under some arbitrary hypothesis ![]() .
.
![]() is given.
Normally,
is given.
Normally,
![]() must be derived analytically.
Only in rare situations can
must be derived analytically.
Only in rare situations can
![]() can be estimated.
We discuss type of problem in Section 2.2.3.
can be estimated.
We discuss type of problem in Section 2.2.3.