We now validate the proposition above, that solving
for the maximum entropy
multivariate truncated exponential (MaxEnt-MTE) distribution
approximates the asymptotic distribution of MCMC-UMS
for doubly-bounded data.
In this experiment, we used a data size of 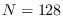 .
The matrix
.
The matrix 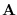 in (5.1)
computed the first
in (5.1)
computed the first 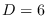 Coefficients of the
length-
Coefficients of the
length- DCT of
DCT of  .
We created a data sample
.
We created a data sample  using a raised sine-wave plus
Gaussian noise, clipped it to the interval [0,1], then computed the feature
using a raised sine-wave plus
Gaussian noise, clipped it to the interval [0,1], then computed the feature 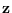 .
The original
.
The original  was then discarded. We then got a starting point
for
was then discarded. We then got a starting point
for
 using a linear programming solver
as previously explained, with the lower and upper bounds of 0 and
using a linear programming solver
as previously explained, with the lower and upper bounds of 0 and 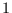 .
We then maximized (7.6) over
.
We then maximized (7.6) over
 subject to (5.12)
using the method above. Figure 7.2 shows the results.
See software/test_lin01.m.
subject to (5.12)
using the method above. Figure 7.2 shows the results.
See software/test_lin01.m.
Figure:
The Maximum entropy
asymptotic mean (dark line) and the sample mean
(circles). One random MCMC-UMS sample is shown (light jagged line).
The pseudo-inverse solution (dotted lin) is seen to
have values outside  .
.
|
|
The sample-mean of MCMC-UMS after 10000 samples matches the
Maximum entropy mean solution as close as could be determined.
![\includegraphics[width=5.2in]{x1x2u2.eps}](img766.png)