Application of SPA to Circular
Auto-Correlation Function Analysis
The auto-correlation function (ACF) is
widely used in auto-regressive (AR) time-series
analysis and spectral estimation [31].
An estimate of the ACF given a length-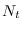 time-series
can be obtained using the frequency-domain
approach by inverse DFT of the
raw spectrum.
Because the FFT is used, this approach falls under
feature extraction methods for
circularly stationary processes
(See section 10.1).
The “input" data
time-series
can be obtained using the frequency-domain
approach by inverse DFT of the
raw spectrum.
Because the FFT is used, this approach falls under
feature extraction methods for
circularly stationary processes
(See section 10.1).
The “input" data  is the
is the
 vector of raw spectral values
(magnitude-squared DFT), where
vector of raw spectral values
(magnitude-squared DFT), where
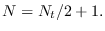 The output ACF feature is
The output ACF feature is
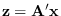 .
To compute the
.
To compute the 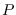 -th order ACF (lags 0 through
-th order ACF (lags 0 through 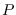 ),
the columns of the
),
the columns of the
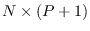 matrix
matrix 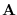 must contain the cosine functions
which are the basis functions for the real part of the inverse FFT.
To properly compute the ACF, we need to effectively
compute the inverse-FFT of the
full length-
must contain the cosine functions
which are the basis functions for the real part of the inverse FFT.
To properly compute the ACF, we need to effectively
compute the inverse-FFT of the
full length-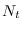 spectrum (redundant bins duplicated) which requires that we
scale the complex bins (
spectrum (redundant bins duplicated) which requires that we
scale the complex bins (
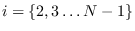 ) by 2.0
and the real bins (
) by 2.0
and the real bins (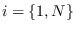 ) by 1.0.
This un-equal bin scaling can be formalized by the scaling
variable
) by 1.0.
This un-equal bin scaling can be formalized by the scaling
variable 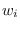 , which takes the values of 1 or 2 as indicated.
The resulting transformation is
, which takes the values of 1 or 2 as indicated.
The resulting transformation is
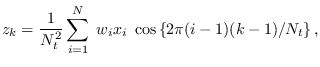 |
(5.4) |
for
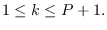 This computes the order-
This computes the order-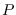 circular ACF using the frequency-domain method.
In this case, the energy statistic is
circular ACF using the frequency-domain method.
In this case, the energy statistic is
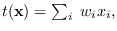 with un-equal bin scaling, which is
a valid norm on
with un-equal bin scaling, which is
a valid norm on
 .
.
There are two possibilities for computation of the
ACF depending on if one is starting with time-series
or spectral data.
In both cases, we may assume that the time-series
is independent Gaussian noise with mean 0 and variance 1.
If  is the time-series, then
is the time-series, then
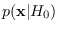 is taken directly from Table 3.1, “Gaussian" row,
and
is taken directly from Table 3.1, “Gaussian" row,
and
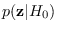 is computed using software/pdf_A_chisq_m.m.
is computed using software/pdf_A_chisq_m.m.
[lpzH0,ic] = pdf_A_chisq_m(z,A,K,[ic]);
where K is an  vector with the degrees of freedom [1,2,2, ... 2,2,1].
See
software/module_acf_spax.m for additional details.
For testing, use
software/module_acf_test.m with TYPE=2.
vector with the degrees of freedom [1,2,2, ... 2,2,1].
See
software/module_acf_spax.m for additional details.
For testing, use
software/module_acf_test.m with TYPE=2.
If  is the raw spectrum,
is the raw spectrum,
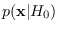 is
given by (4.1), with
is
given by (4.1), with  taking the role of
taking the role of  in the equation, and
in the equation, and
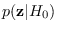 is computed using software/pdf_A_chisq_m.m.
For additional details, see software/module_acf_spa.m.
For re-synthesis, use software/module_acf_synth.m.
For testing, use software/module_acf_test.m with TYPE=0.
is computed using software/pdf_A_chisq_m.m.
For additional details, see software/module_acf_spa.m.
For re-synthesis, use software/module_acf_synth.m.
For testing, use software/module_acf_test.m with TYPE=0.
![]() is the time-series, then
is the time-series, then
![]() is taken directly from Table 3.1, “Gaussian" row,
and
is taken directly from Table 3.1, “Gaussian" row,
and
![]() is computed using software/pdf_A_chisq_m.m.
is computed using software/pdf_A_chisq_m.m.
![]() is the raw spectrum,
is the raw spectrum,
![]() is
given by (4.1), with
is
given by (4.1), with ![]() taking the role of
taking the role of ![]() in the equation, and
in the equation, and
![]() is computed using software/pdf_A_chisq_m.m.
For additional details, see software/module_acf_spa.m.
For re-synthesis, use software/module_acf_synth.m.
For testing, use software/module_acf_test.m with TYPE=0.
is computed using software/pdf_A_chisq_m.m.
For additional details, see software/module_acf_spa.m.
For re-synthesis, use software/module_acf_synth.m.
For testing, use software/module_acf_test.m with TYPE=0.