Magnitude Squared DFT of Gaussian data
This building block considers the DFT of Gaussian data followed by the
computation of the magnitude-squared of the bins.
Like the previous example, this belongs to a general class of chi-squared
feature extractors fitting within the “Gaussian" row of Table 3.1.
The energy statistic in all of these problems is the total energy.
In the case of DFT magnitude-squared,
the ES is contained implicitly (Parseval's theorem).
Let  be even and
be even and
The DFT bins are independent under 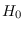 , but not identically
distributed. DFT bins 0 and
, but not identically
distributed. DFT bins 0 and 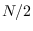 are real-valued so
are real-valued so
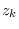 have the Chi-squared distribution with 1 degree of freedom
scaled by
have the Chi-squared distribution with 1 degree of freedom
scaled by  , which we denote by
, which we denote by 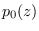 :
:
DFT bins 1 through 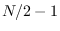 are complex
so
are complex
so 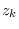 have the Chi-squared
distribution with 2 degrees of freedom scaled by
have the Chi-squared
distribution with 2 degrees of freedom scaled by 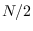 ,
which we denote by
,
which we denote by 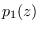 :
:
The complete PDF
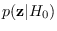 is
is
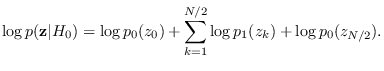 |
(4.1) |
The J-function,
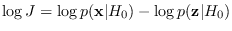 can be simplified for even
can be simplified for even  to
to
which interestingly is data independent except with respect to the zero
and Nyquist frequency bins.
For more information, refer to the software module
software/module_dftmsq.m.
Re-synthesis of  from
from 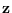 using UMS (Section 3.3)
is accomplished first by taking the square-root
of each bin. We then multiply the zero and Nyquist
bins (
using UMS (Section 3.3)
is accomplished first by taking the square-root
of each bin. We then multiply the zero and Nyquist
bins (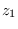 and
and 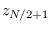 for even
for even  ) by 1 or -1,
each with probability 1/2.
The remaining bins are multiplied by a phase term
) by 1 or -1,
each with probability 1/2.
The remaining bins are multiplied by a phase term
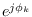 , where
, where 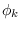 are independent RV uniformly
distributed on the interval
are independent RV uniformly
distributed on the interval
![$[0,\;2\pi]$](img414.png) .
Finally, the length-
.
Finally, the length- DFT vector is created
by appending the conjugate of the complex bins, then
taking the inverse DFT to obtain
DFT vector is created
by appending the conjugate of the complex bins, then
taking the inverse DFT to obtain  .
For more information, refer to the software module
software/module_dftmsq_synth.m.
.
For more information, refer to the software module
software/module_dftmsq_synth.m.
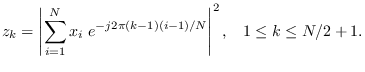
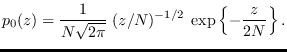
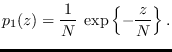
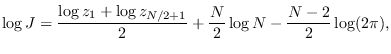
![]() from
from ![]() using UMS (Section 3.3)
is accomplished first by taking the square-root
of each bin. We then multiply the zero and Nyquist
bins (
using UMS (Section 3.3)
is accomplished first by taking the square-root
of each bin. We then multiply the zero and Nyquist
bins (![]() and
and ![]() for even
for even ![]() ) by 1 or -1,
each with probability 1/2.
The remaining bins are multiplied by a phase term
) by 1 or -1,
each with probability 1/2.
The remaining bins are multiplied by a phase term
![]() , where
, where ![]() are independent RV uniformly
distributed on the interval
are independent RV uniformly
distributed on the interval
![]() .
Finally, the length-
.
Finally, the length-![]() DFT vector is created
by appending the conjugate of the complex bins, then
taking the inverse DFT to obtain
DFT vector is created
by appending the conjugate of the complex bins, then
taking the inverse DFT to obtain ![]() .
For more information, refer to the software module
software/module_dftmsq_synth.m.
.
For more information, refer to the software module
software/module_dftmsq_synth.m.