UMS
We now consider UMS - that is
to generate samples of data which will have
exactly the specified ML parameter estimates,
uniformly on the manifold.
Given fixed MLE values of
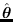 ,
,
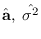 ,
the we can easily define the manifold of all
,
the we can easily define the manifold of all  that lead to the
given MLE as follows. Define the statistics
that lead to the
given MLE as follows. Define the statistics
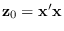 ,
,
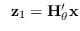 ,
and
,
and
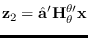 .
We can use (4.2), and (4.3) to compute
.
We can use (4.2), and (4.3) to compute
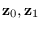 .
The ML estimates
.
The ML estimates
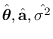 are such that the partial derivative of
are such that the partial derivative of
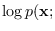
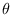
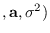 with respect
to each parameter is zero. The derivative constraint for
with respect
to each parameter is zero. The derivative constraint for
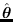 leads to
leads to
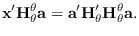 |
(4.7) |
We can use (4.7) to compute 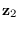 .
So, we are able to compute
.
So, we are able to compute
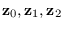 just from
just from
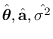 .
The equations defining
.
The equations defining
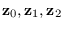 lead
to a set of constraints for
lead
to a set of constraints for  that can be written in the form
that can be written in the form
where
![${\bf A}=[{\bf H}_\theta \;\; \hat{{\bf a}}^\prime {\bf H}_\theta^{\theta}].$](img509.png) This is the problem of Section 4.4. We can apply the results
of that Section to sample the manifold. Every sample will meet the derivative constraint
for
This is the problem of Section 4.4. We can apply the results
of that Section to sample the manifold. Every sample will meet the derivative constraint
for
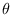 as well as produce the same amplitude and variance estimates,
so will produce the given ML solution. See
software/test_ml.m for an example
of sinusoidal frequency estimation.
See also Section 9.2.3 for an example of this method.
as well as produce the same amplitude and variance estimates,
so will produce the given ML solution. See
software/test_ml.m for an example
of sinusoidal frequency estimation.
See also Section 9.2.3 for an example of this method.