Next: First derivatives Up: Gaussian Model with Non-Linear Previous: Data model Contents
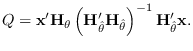
Alternatively, the Newton-Raphson algorithm may be used to find
![]() as described in Section 17.5.
For this we need the first derivatives and Fisher's information (See Section 17.5).
as described in Section 17.5.
For this we need the first derivatives and Fisher's information (See Section 17.5).