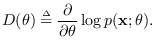Maximum Likelihood Parameter Estimation and the CR bound
Consider a general log PDF that depends on 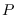 parameters:
parameters:
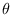
![$= [\theta_1, \theta_2 \ldots \theta_P]^\prime$](img1918.png) :
:
The Fisher's information between any two parameters 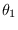 and
and 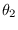 is defined by
is defined by
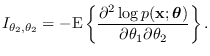 |
(17.13) |
Collecting all these values into the matrix
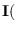
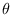
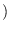 ,
we have the Fisher's information matrix. The Cramer-Rao lower bound states
that the covariance matrix
,
we have the Fisher's information matrix. The Cramer-Rao lower bound states
that the covariance matrix 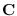 of any joint unbiased estimator
for the parameters
of any joint unbiased estimator
for the parameters
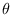 is such that
is such that
. This
effectively means that
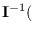
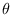
 is the lower bound for
the covariance of any unbiased estimator.
is the lower bound for
the covariance of any unbiased estimator.
The inverse of the Fisher's information matrix is a good estimate
of the parameter estimation error covariance and is useful for
iterative optimization. Given a parameter estimate
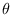
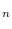 , the new estimate
is obtained as
, the new estimate
is obtained as
where
is the gradient vector formed from the first partial derivatives
It is possible to optimize only subsets of the features as well. A feature pair
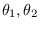 is updated according to
is updated according to
![$\displaystyle \left[ \begin{array}{l} \theta_1 \theta_2 \end{array}\right]_{...
...^{-1}
\; \left[ \begin{array}{l} D(\theta_1) D(\theta_2) \end{array}\right].$](img1928.png) |
(17.15) |
![]()
![]() , the new estimate
is obtained as
, the new estimate
is obtained as