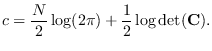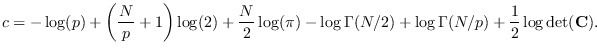Non-Gaussian

The multi-variate Gaussian (17.3) can be thought of as one member of a class of PDFs

$$\log p({\bf x}) = - \frac{1}{2} \left[\left({\bf x}- \mbox{\boldm... ...; {\bf C}^{-1} \; \left({\bf x}- \mbox{\boldmath$\mu$}\right) \right]^{p/2} -c,$$ (17.11)

where for Gaussian, $p=2$ and

$$c= \frac{N}{2}\log(2\pi) +\frac{1}{2} \log {\rm det}({\bf C}).$$

For arbitrary $p$, we have

$$c = -\log(p) + \left(\frac{N}{p}+1\right) \log(2) + \frac{N}{2}\l... ...pi) - \log\Gamma(N/2) + \log\Gamma(N/p) +\frac{1}{2} \log {\rm det}({\bf C}).$$

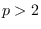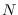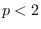For $p>2$, the distribution tends to a flat-topped elliptical plate in $N$-space with sharp shoulders. For $p<2$, the distribution has higher tails. These non-Gaussian distributions may be useful in some applications where tail behavior needs to be modified.