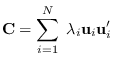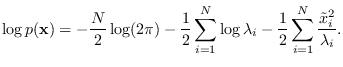Next: Multivariate Gaussian in Frequency Up: Multivariate PDFs Previous: Multivariate PDFs Contents
The multivariate Gaussian PDF of dimension ![]() with mean
with mean
![]() and covariance
and covariance
![]() is:
is:
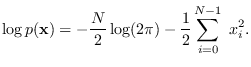
Note that if we know the eigendeomposition of ![]() , we may write (17.3)
in a simpler form. Since
, we may write (17.3)
in a simpler form. Since ![]() is a symmetric positive definite matrix,
the eigenvectors form a complete orthogonal subspace on
is a symmetric positive definite matrix,
the eigenvectors form a complete orthogonal subspace on
![]() . Let
. Let