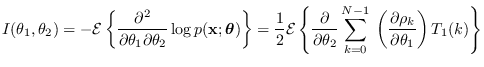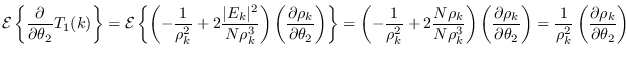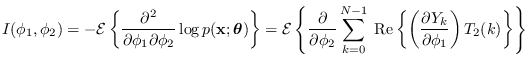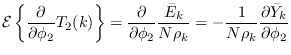Parameter Estimation
Equation (17.6) is useful for parameter estimation. Let
the mean 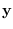 depend on a set of mean parameters
depend on a set of mean parameters
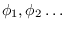 ,
and let the spectrum values
,
and let the spectrum values
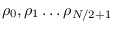 depend on
spectral parameters
depend on
spectral parameters
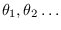 . Let
the first derivatives of
. Let
the first derivatives of
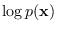 be denoted by
be denoted by
We have
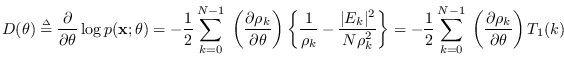 |
(17.7) |
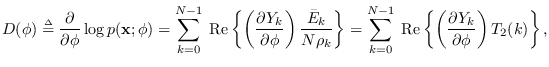 |
(17.8) |
where
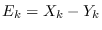 , and
, and 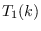 ,
, 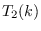 are defined implicitly.
are defined implicitly.
Using (17.7), the Fisher's information between spectral parameters 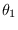 and
and 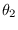 equals
equals
Before carrying out the derivative with respect to 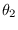 , notice that
, notice that
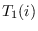 is zero in expected value. Therefore, the only terms remaining are
associated with the derivative of
is zero in expected value. Therefore, the only terms remaining are
associated with the derivative of 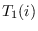 . Note that
. Note that
Therefore,
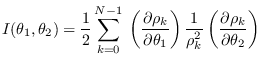 |
(17.9) |
Using (17.8), for “mean" parametrs,
Before carrying out the derivative with respect to 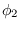 , notice that
, notice that
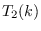 is zero in expected value. Therefore, the only terms remaining are
associated with the derivative of
is zero in expected value. Therefore, the only terms remaining are
associated with the derivative of 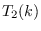 . Note that
. Note that
Therefore,
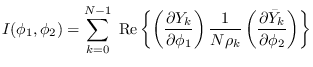 |
(17.10) |
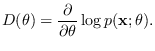
![]() and
and ![]() equals
equals