Computation of likelihood function using Proxy HMM
To implement (14.1), (14.2) brute-force is obviously
impractical because of the combinatorial number of
state sequences 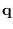 , but we can use the proxy HMM to do it efficiently.
Note that each segmentation
, but we can use the proxy HMM to do it efficiently.
Note that each segmentation 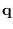 corresponds to a distinct
path through the proxy HMM state trellis, which has probability
given by equation (14) in [65].
If we had the likelihood functions of each base-segment of
the proxy HMM, the proxy likelihood function would be
corresponds to a distinct
path through the proxy HMM state trellis, which has probability
given by equation (14) in [65].
If we had the likelihood functions of each base-segment of
the proxy HMM, the proxy likelihood function would be
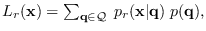 where
where 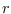 stands for “p(r)oxy", and where
stands for “p(r)oxy", and where
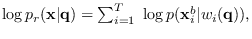 where
where
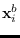 is the
is the 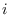 -th base segment and
-th base segment and
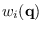 is the proxy HMM state at time step
is the proxy HMM state at time step 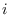 corresponding
to segmentation
corresponding
to segmentation 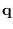 .
The well-known HMM forward procedure [65]
calculates the total proxy likelihood function
.
The well-known HMM forward procedure [65]
calculates the total proxy likelihood function
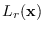 efficiently using dynamic programming and without enumerating the
segmentations.
efficiently using dynamic programming and without enumerating the
segmentations.
But the proxy log likelihood functions
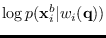 are defined for a single base segment, whereas
the MR-HMM segment log-likelihood functions
are defined for a single base segment, whereas
the MR-HMM segment log-likelihood functions
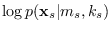 are defined for segments spanning
are defined for segments spanning 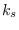 base segments.
This problem is solved by writing
base segments.
This problem is solved by writing
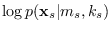 as a sum of
as a sum of 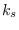 equal parts:
equal parts:
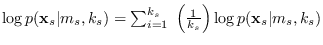 ,
where each part is assumed to apply to just one base segment,
so can be used in place of the proxy segment log-likelihood functions.
This substitution forces the proxy HMM forward procedure
to compute
,
where each part is assumed to apply to just one base segment,
so can be used in place of the proxy segment log-likelihood functions.
This substitution forces the proxy HMM forward procedure
to compute
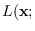
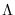
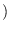 for the the MR-HMM.
This substitution can be more precicely written as
for the the MR-HMM.
This substitution can be more precicely written as
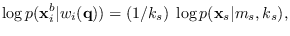 |
(14.3) |
where for segmentation 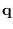 , base segment time
, base segment time 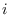 lies within
segment
lies within
segment 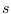 of length
of length 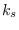 .
The classical forward procedure applied to the
proxy HMM then produces
.
The classical forward procedure applied to the
proxy HMM then produces
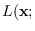
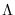
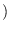 .
Furthermore, by calculating the backward procedure
on the proxy HMM and combining with the forward procedure, we obtain
the gamma probability
.
Furthermore, by calculating the backward procedure
on the proxy HMM and combining with the forward procedure, we obtain
the gamma probability
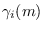 , which is the
a posteriori probability
that the system is in proxy state
, which is the
a posteriori probability
that the system is in proxy state 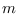 at base segment
at base segment 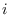 given all the available data.
This is illustrated in Figure 14.1 as the
filled-in circles in the proxy state trellis.
These filled-in circles correspond to when
given all the available data.
This is illustrated in Figure 14.1 as the
filled-in circles in the proxy state trellis.
These filled-in circles correspond to when
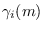 has a high value.
In the gap between the two pulses, is a case
when probability is shared between more than one
candidate path. If we sum up all the gamma probabilities
for a given sub-class, we get an indication of the
probability of each sub-class (illustrated at very bottom
of Figure 14.1).
has a high value.
In the gap between the two pulses, is a case
when probability is shared between more than one
candidate path. If we sum up all the gamma probabilities
for a given sub-class, we get an indication of the
probability of each sub-class (illustrated at very bottom
of Figure 14.1).
![]() are defined for a single base segment, whereas
the MR-HMM segment log-likelihood functions
are defined for a single base segment, whereas
the MR-HMM segment log-likelihood functions
![]() are defined for segments spanning
are defined for segments spanning ![]() base segments.
This problem is solved by writing
base segments.
This problem is solved by writing
![]() as a sum of
as a sum of ![]() equal parts:
equal parts:
![]() ,
where each part is assumed to apply to just one base segment,
so can be used in place of the proxy segment log-likelihood functions.
This substitution forces the proxy HMM forward procedure
to compute
,
where each part is assumed to apply to just one base segment,
so can be used in place of the proxy segment log-likelihood functions.
This substitution forces the proxy HMM forward procedure
to compute
![]()
![]()
![]() for the the MR-HMM.
This substitution can be more precicely written as
for the the MR-HMM.
This substitution can be more precicely written as