Reestimation of Gaussian Mixture Parameters
If 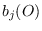 are modeled as Gaussian mixtures (GM), one could simply
determine the weighted ML estimates of the GM parameters. Since only
iterative methods are known, this would require iterating
to convergence at each step. A more global approach is
possible if the mixture component assignments are
regarded as “missing data" [66]. The result is
that the quantity
are modeled as Gaussian mixtures (GM), one could simply
determine the weighted ML estimates of the GM parameters. Since only
iterative methods are known, this would require iterating
to convergence at each step. A more global approach is
possible if the mixture component assignments are
regarded as “missing data" [66]. The result is
that the quantity
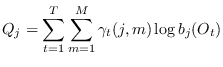 |
(13.19) |
is maximized, where
![$\displaystyle \gamma_t(j,m) =
w_{t,j} \left[ \frac{\displaystyle
c_{jm} \; {\ca...
...c_{jk} \; {\cal N}({\bf O}_t,\mbox{\boldmath$\mu$}_{jk},{\bf U}_{jk})
} \right]$](img1630.png) |
(13.20) |
The weights
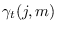 are interpreted as the
probability that the Markov chain is in state
are interpreted as the
probability that the Markov chain is in state 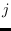 and the observation is from mixture component
and the observation is from mixture component 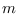 at time
at time 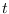 .
The resulting update equations for
.
The resulting update equations for
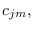
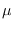
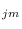 , and
, and
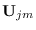 are
computed as follows:
are
computed as follows:
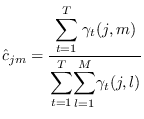 |
(13.21) |
Note the similarity to (13.2). This means that the algorithms
designed for Gaussian mixtures are applicable for updating the
state PDFs of the HMM.
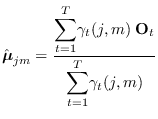 |
(13.22) |
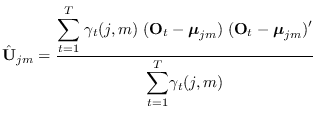 |
(13.23) |
Note that the above equations do not treat the problem
of constraining the GM covariances. This needs to be
addressed (see section 13.2).