Let
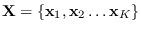 be a collection of data.
The Q-function is defined as the expected “complete" log-PDF where
the expectation is carried out over the conditional distribution
of the “missing data", given
be a collection of data.
The Q-function is defined as the expected “complete" log-PDF where
the expectation is carried out over the conditional distribution
of the “missing data", given 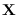 , using the current best estimate of the
PDF parameters
, using the current best estimate of the
PDF parameters 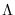 , and the log-PDF is written in terms of the
new values of the parameters to be estimated,
, and the log-PDF is written in terms of the
new values of the parameters to be estimated,
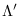 :
:
Expanding,
where
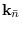 are
are the assignments not associated with sample
are
are the assignments not associated with sample 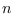 .
The inner summation is a marginalization
.
The inner summation is a marginalization
Thus,
where the conditional model probabilities
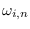 are defined as
are defined as
The maximization of
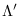 can be carried out on the quantity
can be carried out on the quantity
where we have added data weights, 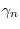 ,
which define a probabilistic weights for each data sample.
This could be interpreted as adjusting the influence of a training sample
as though sample
,
which define a probabilistic weights for each data sample.
This could be interpreted as adjusting the influence of a training sample
as though sample 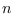 was replicated
was replicated 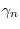 times, or can be thought
of as the probabilistic certainty that sample
times, or can be thought
of as the probabilistic certainty that sample 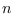 is indeed valid.
By collecting
is indeed valid.
By collecting 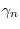 and
and
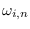 together
into a quantity
together
into a quantity 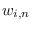 , we have
, we have
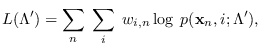 |
(13.2) |
where
The algorithm in Table 13.1, maximizes (13.2) over
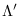 at each iteration.
While correct, it is representative only. Actual
computation requires careful attention to
numerical issues which are discussed below.
at each iteration.
While correct, it is representative only. Actual
computation requires careful attention to
numerical issues which are discussed below.
Table 13.1:
Update Equations for Gaussian Mixtures. This is
representative only. Actual implementation requires attention to
numerical issues discussed in the text.
 |
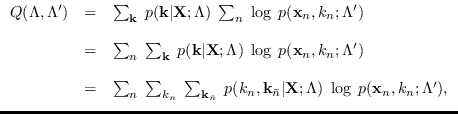
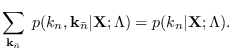
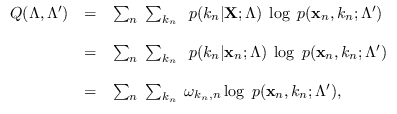
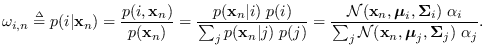
![]() at each iteration.
While correct, it is representative only. Actual
computation requires careful attention to
numerical issues which are discussed below.
at each iteration.
While correct, it is representative only. Actual
computation requires careful attention to
numerical issues which are discussed below.
