The standard HMM
Following the notation of Rabiner [65],
there are 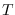 observation times. At each time
observation times. At each time
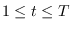 ,
there is a discrete state variable
,
there is a discrete state variable 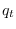 which takes one of
which takes one of  values
values
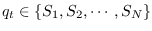 .
According to the Markovian assumption, the probability
distribution of
.
According to the Markovian assumption, the probability
distribution of 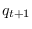 depends only on the value
of
depends only on the value
of 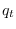 . This is described compactly as a state transition
probability matrix
. This is described compactly as a state transition
probability matrix 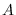 whose elements
whose elements 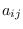 represent the
probability that
represent the
probability that 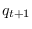 equals
equals 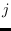 given
that
given
that 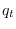 equals
equals 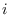 . The initial state probabilities
are denoted
. The initial state probabilities
are denoted 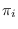 , the probability that
, the probability that
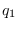 equals
equals 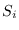 .
.
It is a hidden Markov model because
the states 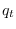 are hidden from view; we cannot observe them.
But, we can observe
the random data
are hidden from view; we cannot observe them.
But, we can observe
the random data 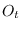 which is generated
according to a PDF dependent on the state at time
which is generated
according to a PDF dependent on the state at time 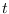 .
We denote the PDF of
.
We denote the PDF of 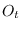 under state
under state 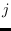 as
as
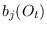 .
.
The complete set of model parameters that define the HMM are
The Baum-Welch algorithm calculates
new estimates 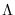 given an observation sequence
given an observation sequence
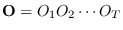 and a previous estimate of
and a previous estimate of 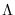 .
The algorithm is composed of two parts: the forward/backward procedure,
and the reestimation of parameters.
.
The algorithm is composed of two parts: the forward/backward procedure,
and the reestimation of parameters.
Subsections
![]() are hidden from view; we cannot observe them.
But, we can observe
the random data
are hidden from view; we cannot observe them.
But, we can observe
the random data ![]() which is generated
according to a PDF dependent on the state at time
which is generated
according to a PDF dependent on the state at time ![]() .
We denote the PDF of
.
We denote the PDF of ![]() under state
under state ![]() as
as
![]() .
.