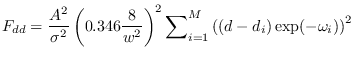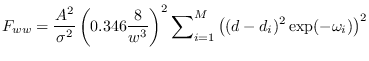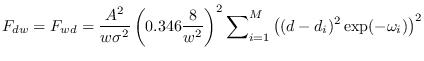The log-PDF of the data 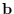 is
is
where
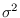 is the variance of the additive independent
Gaussian noise. The components of the Fisher Information
Matrix (FIM) for PDF parameters
is the variance of the additive independent
Gaussian noise. The components of the Fisher Information
Matrix (FIM) for PDF parameters
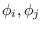 are given by
are given by
Let the FIM be given by
A standard CR bound analysis [64] produces
where
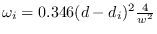 .
The CR bound matrix is given by
.
The CR bound matrix is given by
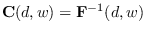 .
.
![$\displaystyle \ln p({\bf b};d,w) =
-\frac{1}{2} \ln (2\pi\sigma^{2}) - \frac{1...
...i} - A \exp\left\{ -0.346 (d-d_{i})^{2}
\frac{4}{w^{2}}\right\} \right] ^{2},
$](img1557.png)
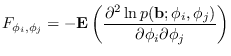
![$\displaystyle F(d,w)= \left[ \begin{array}{ll}
F_{dd} & F_{dw}\\
F_{wd} & F_{ww} \\
\end{array} \right].
$](img1561.png)