Assume that beam intensity values are available from a set
of 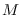 uniformly spaced (in direction)
sonar or radar beams. A target exists somewhere
in the span of the
uniformly spaced (in direction)
sonar or radar beams. A target exists somewhere
in the span of the 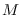 beams, yet we do not know its
center location, nor do we know the width of the response to the
signal (as in a broadband system with frequency-dependent
beamwidth). We assume for simplicity that
the amplitude is known, yet in principle,
amplitude can be another unknown.
Thus, there are two parameters we seek to
estimate: direction
beams, yet we do not know its
center location, nor do we know the width of the response to the
signal (as in a broadband system with frequency-dependent
beamwidth). We assume for simplicity that
the amplitude is known, yet in principle,
amplitude can be another unknown.
Thus, there are two parameters we seek to
estimate: direction 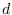 and beamwidth
and beamwidth 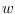 . This problem
normally requires a search in the
. This problem
normally requires a search in the 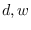 plane for best match
(as in maximum likelihood). Using GM, we solve the problem
without a search, yet achieve performance comparable to ML!
plane for best match
(as in maximum likelihood). Using GM, we solve the problem
without a search, yet achieve performance comparable to ML!
Let the beam pointing directions
be
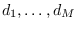 . Let the beam
intensities
. Let the beam
intensities
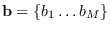 be modeled by
be modeled by
where 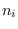 is a noise term (we use Gaussian noise in the
simulation and CR bound analysis). This is a Gaussian
beampattern with 3 dB width
is a noise term (we use Gaussian noise in the
simulation and CR bound analysis). This is a Gaussian
beampattern with 3 dB width 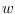 .
.
A sample size of 4096 was created using 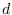 and
and 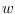 selected from
uniform distributions in the ranges [-10,10], [15,50],
respectively. Parameters were
selected from
uniform distributions in the ranges [-10,10], [15,50],
respectively. Parameters were 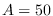 ,
,
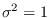 ,
, 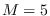 ,
,
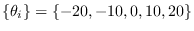 .
A GM model
.
A GM model
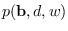 of
12 modes was trained on the data.
To illustrate the ability to create
conditional distributions,
of
12 modes was trained on the data.
To illustrate the ability to create
conditional distributions,
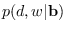 was computed for a sample of
was computed for a sample of 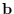 computed for
computed for 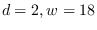 with no additive noise.
The result appears in Figure 13.6.
The visual effect of this figure is to say to the
operator that there are no other values of interest
except the peak.
with no additive noise.
The result appears in Figure 13.6.
The visual effect of this figure is to say to the
operator that there are no other values of interest
except the peak.
Figure:
Condition distibution of 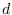 (THTA) and
(THTA) and
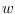 (WDTH) given a sample of
(WDTH) given a sample of 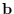 computed for
computed for 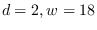 with no additive noise.
with no additive noise.
|
|
It is also possible to condition on 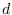 or
or 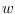 .
The conditional
distribution
.
The conditional
distribution
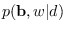 was computed for
was computed for 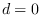 and
and 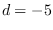 . these plots are shown in Figures
13.7,13.8.
. these plots are shown in Figures
13.7,13.8.
Figure:
The condition distibution
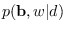 marginalized on each dimension of
marginalized on each dimension of 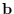 for
for 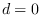 .
.
|
|
Figure:
The condition distibution
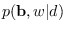 marginalized on each dimension of
marginalized on each dimension of 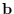 for
for 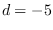 .
.
|
|
Note that the beam output values have distributions
symmetric about the value of 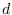 , as expected. Note
also the wider spread of values on outer beams due to the
variations in
, as expected. Note
also the wider spread of values on outer beams due to the
variations in 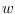 .
.
Estimates of 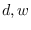 were obtained
using formulas (13.8),(13.6).
To determine bias,
uncorrupted (no noise) values of
were obtained
using formulas (13.8),(13.6).
To determine bias,
uncorrupted (no noise) values of 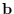 were
created for a range of
were
created for a range of 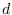 for
for 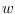 fixed at 20,
and for a range of
fixed at 20,
and for a range of 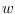 for
for 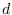 fixed at 2. These two
graphs appear in Figures 13.9,13.10.
fixed at 2. These two
graphs appear in Figures 13.9,13.10.
Figure:
Plot of 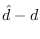 for noise-free data
with
for noise-free data
with 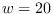 .
.
|
|
Figure:
Plot of 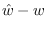 for noise-free data
with
for noise-free data
with 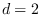 .
.
|
|
In each case, the bias error is plotted as
a function of the variable parameter.
Bias is clearly a function of the operating point. It is
also a function of the number of modes and the convergence point
of the GM approximation algorithm.
Random error was determined by choosing a specific
value of 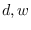 and running 300 trials with independent noise added to
and running 300 trials with independent noise added to
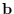 . The result of 300 trials is shown below.
. The result of 300 trials is shown below.
| |
True Value |
Mean |
Variance |
CR Bound |
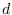 |
2 |
1.9435 |
.0550 |
.0493 |
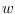 |
18 |
18.003 |
.09756 |
.0945 |
Results of 300 trials,
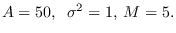
The results were in close agreement
with the CR bound. Strictly speaking, the CR bound does
not apply since the conditional mean estimator is biased
for a fixed 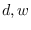 (it is unbiased for random
(it is unbiased for random 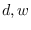 conditioned
on
conditioned
on 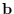 ), however, the CR bound is useful for comparison
purposes.
), however, the CR bound is useful for comparison
purposes.
![]() . Let the beam
intensities
. Let the beam
intensities
![]() be modeled by
be modeled by
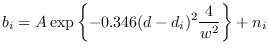
![]() and
and ![]() selected from
uniform distributions in the ranges [-10,10], [15,50],
respectively. Parameters were
selected from
uniform distributions in the ranges [-10,10], [15,50],
respectively. Parameters were ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
A GM model
.
A GM model
![]() of
12 modes was trained on the data.
To illustrate the ability to create
conditional distributions,
of
12 modes was trained on the data.
To illustrate the ability to create
conditional distributions,
![]() was computed for a sample of
was computed for a sample of ![]() computed for
computed for ![]() with no additive noise.
The result appears in Figure 13.6.
The visual effect of this figure is to say to the
operator that there are no other values of interest
except the peak.
with no additive noise.
The result appears in Figure 13.6.
The visual effect of this figure is to say to the
operator that there are no other values of interest
except the peak.
![\includegraphics[width=3.5in,height=3.5in, clip]{fig22.eps}](img1549.png)
![]() or
or ![]() .
The conditional
distribution
.
The conditional
distribution
![]() was computed for
was computed for ![]() and
and ![]() . these plots are shown in Figures
13.7,13.8.
. these plots are shown in Figures
13.7,13.8.
![]() were obtained
using formulas (13.8),(13.6).
To determine bias,
uncorrupted (no noise) values of
were obtained
using formulas (13.8),(13.6).
To determine bias,
uncorrupted (no noise) values of ![]() were
created for a range of
were
created for a range of ![]() for
for ![]() fixed at 20,
and for a range of
fixed at 20,
and for a range of ![]() for
for ![]() fixed at 2. These two
graphs appear in Figures 13.9,13.10.
fixed at 2. These two
graphs appear in Figures 13.9,13.10.