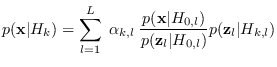Class-Specific Feature Mixture (CSFM)
To get around the one class, one feature assumption,
CSFM assumes that each class 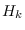 is composed of
is composed of 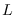 sub-classes
represented by an additive mixture PDF. We assume
that class
sub-classes
represented by an additive mixture PDF. We assume
that class 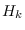 is composed of
is composed of 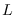 subclasses
subclasses
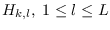 , that have relative probabilities of
occurrence
, that have relative probabilities of
occurrence
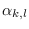 and individual sub-class PDFs
and individual sub-class PDFs
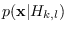 .
The mixture PDF for
.
The mixture PDF for 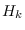 is given by:
is given by:
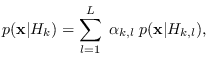 |
(12.5) |
where
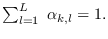 If we assume that each sub-class has a different feature
(approximate sufficient statistic) to distinguish it from
a sub-class dependent reference hypothesis
If we assume that each sub-class has a different feature
(approximate sufficient statistic) to distinguish it from
a sub-class dependent reference hypothesis 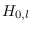 , we
apply (2.2) to get
, we
apply (2.2) to get
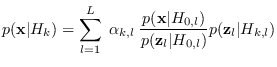 |
(12.6) |
Note that each class PDF is represented by the same library of 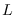 models.
The CSFM classifier is
models.
The CSFM classifier is
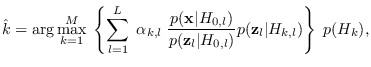 |
(12.7) |
which may be interpreted as a
data-specific feature classifier because
for each data sample  , the factor
, the factor
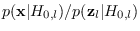 has a dominant effect, effectively picking one feature
to classfy the sample.
has a dominant effect, effectively picking one feature
to classfy the sample.