Estimating the AR coefficients - deterministic approach (Levinson Algorithm)

Compared to ARMA and MA, AR has the advantage that closed-form approximate ML estimates can be found. One way is to regard the problem as a least-squares problem. Suppose $N$ samples of some AR data is available. Let (10.39) be written in matrix form

$$\left[ \begin{array}{r} x_N x_{N-1} x_{N-2} \vdots \end{... ...ight] \left[ \begin{array}{r} a_1 a_2 \vdots a_P \end{array}\right],$$

or in matrix form

$${\bf x}= {\bf X} \; {\bf a}.$$

The least squares estimate of ${\bf a}$ is (see 17.12),

$$\hat{{\bf a}} = ({\bf X}^\prime {\bf X})^{-1} {\bf X}^\prime {\bf x}.$$

If we define the ACF estimates

$$\hat{{\bf r}}_P ={1\over N} {\bf X}^\prime {\bf x}, \;\;\; \hat{\bf R}_P = {1\over N} {\bf X}^\prime {\bf X},$$

we have

$$\hat{{\bf a}} = \hat{{\bf R}}^{-1}_P \hat{{\bf r}}_P.$$ (10.44)

Thus, it can be seen that the AR coefficients can be obtained by solving a linear equation involving only ACF estimates. If the circular AR process is assumed, the equation is in terms of circular ACF estimates.

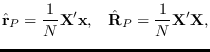
If the ACF estimates are replaced by the true ACF, the relationship holds exactly and is called the Yule-Walker equations. The Yule-Walker equation relates the AR coefficients to the ACF coefficients as follows (example of $P=3$ shown):

$$\left[ \begin{array}{r} a_1 a_2 a_3 \end{array}\right] = -... ...r_3 \end{array}\right], \;\;\;\;\;\;\; \sigma^2 = \sum_{i=0}^P \; a_i \; r_i.$$

Or in matrix notation

$${\bf a}_P = - {\bf R}_P^{-1} \; {\bf r}_P, \;\;\;\;\;\; \sigma^2 = {\bf a}^\prime {\bf r},$$

where

$${\bf r}= [r_0 \; r_1 \ldots r_P], \; {\bf r}_P = [ r_1 \ldots r_P],$$

$${\bf a}= [1 \; a_1 \ldots a_P], \; {\bf a}_P = [ a_1 \ldots a_P].$$

The matrix ${\bf R}_P$ is the $P$-by-$P$ autocorrelation matrix and is a symmetric Toeplitz matrix (constant along any diagonal). The solution of the Yule-Walker equation can be obtained most efficiently using the Levinson-Durbin recursion (MATLAB levinson function) [31].

Now we have come full-circle. From the original AR coefficients, we can write the theoretical power spectrum (10.8), which through the inverse FT becomes the theoretical ACF (10.1), which through the Yule-Walker equations and the Levinson algorithm becomes the AR coefficients again. Note that the Levinson algorithm also produces the reflection coefficients (RC) as a by-product [31]. If estimates of the ACF are used in place of the theoretical ACF, we obtain estimates of the AR coefs. These AR coefficient estimates can then be transformed into an AR power spectrum estimate. Note that the AR model has the “ACF-matching" property that the theoretical ACF corresponding to the AR coefs will match the ACF estimates up to lag $P$ [31]. Note that MATLAB examples in this section can be found in software/ar_example.m.