Data PDF of Circular ARMA process
Based on (17.5), (10.9), we may write
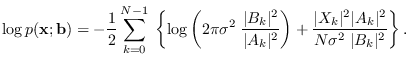 |
(10.18) |
Note that although (10.18) is written in terms of the frequency domain
quantity 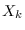 , it is a PDF of
, it is a PDF of  and integrates to precicely 1
over
and integrates to precicely 1
over  in
in
 .
The circular ARMA process is useful for CR bound analysis
and as a way to obtain ML ARMA parameter estimates because it is more tractable than
(10.6).
.
The circular ARMA process is useful for CR bound analysis
and as a way to obtain ML ARMA parameter estimates because it is more tractable than
(10.6).
A simplification is possible for large 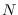 valid for circular ARMA processes.
Note that
valid for circular ARMA processes.
Note that
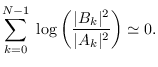 |
(10.19) |
Problem 1
Show (10.19). Hint: write the time-domain equivalent of
(10.18) (similar to section 10.2.3 but with circulant matrix 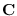 ),
then note that the determinant of
),
then note that the determinant of 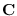 is approximated by
is approximated by
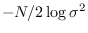 .
From there, deduce the result.
.
From there, deduce the result.
![]() valid for circular ARMA processes.
Note that
valid for circular ARMA processes.
Note that