Data PDF of circularly stationary process
For the circularly stationary process, equation (10.6) may also be used
but the matrix 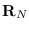 will not be Toeplitz, it will be circulant.
A nice property of circulant matrices is that their eigenvectors are the DFT
basis functions. As a result, (10.6) can be written in the
discrete frequency-domain in terms of the circular power spectrum
will not be Toeplitz, it will be circulant.
A nice property of circulant matrices is that their eigenvectors are the DFT
basis functions. As a result, (10.6) can be written in the
discrete frequency-domain in terms of the circular power spectrum 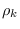 :
:
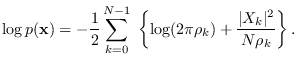 |
(10.7) |
Note well that although (10.7) is written in terms of 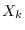 , it is
a PDF of
, it is
a PDF of  . It is only necessary to substitute (10.5) for
. It is only necessary to substitute (10.5) for 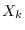 to write the
PDF in terms of
to write the
PDF in terms of  . Then, when integrated over the
. Then, when integrated over the  -dimensional space of
-dimensional space of  , it gives 1.
The circular stationary process has some very nice properties.
It can be shown that the assumption of a circular stationary process means that the DFT coefficients
, it gives 1.
The circular stationary process has some very nice properties.
It can be shown that the assumption of a circular stationary process means that the DFT coefficients
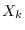 are independent random variables.
This has to do with the fact that the eigenvectors of the covariance matrix
of
are independent random variables.
This has to do with the fact that the eigenvectors of the covariance matrix
of  , which is a circulant matrix, are the DFT basis vectors.
An entire class of PDFs is created when an arbitrary
positive function
, which is a circulant matrix, are the DFT basis vectors.
An entire class of PDFs is created when an arbitrary
positive function 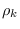 is used - the
expression remains a PDF defined in
is used - the
expression remains a PDF defined in  (See eq. 17.5).
In other words, if we assume the DFT bins are independent
and obey (10.4) for any function
(See eq. 17.5).
In other words, if we assume the DFT bins are independent
and obey (10.4) for any function 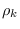 , we obtain an
exact and tractable expression for the PDF of a circularly stationary process
, we obtain an
exact and tractable expression for the PDF of a circularly stationary process  (See Eq. 17.5).
This model can be used to approximate the
PDF of any stationary process whose power spectrum is known.
(See Eq. 17.5).
This model can be used to approximate the
PDF of any stationary process whose power spectrum is known.