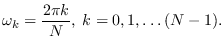Circularly-stationary process
Equation (10.1) is of limited value in practice because
it concerns infinite-length sequences and continuous-valued
frequency. The theory of stationary processes
can be adapted to finite-length time-records if we use the
discrete Fourier transform in place of the
Fourier transform. The concept of stationarity changes
to circular-stationarity.
Analogous to the Wiener-Kinchine theorem (10.1),
the circular power spectrum is defined using the DFT pair
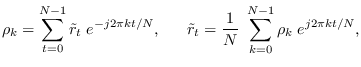 |
(10.2) |
where
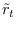 is the circular ACF
is the circular ACF
![$\displaystyle r_k = \frac{1}{N} \sum_{i=1}^N \; x_i x_{[i+k]_N},$](img1075.png) |
(10.3) |
where ![$[i+k]_N$](img1076.png) means modulo-
means modulo- .
.
For a periodic process 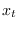 that has a circular ACF, a circularly
stationary process, the circular power spectrum is also defined by
that has a circular ACF, a circularly
stationary process, the circular power spectrum is also defined by
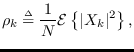 |
(10.4) |
where 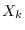 is the
is the  -sample DFT of the length-
-sample DFT of the length- sequence
sequence 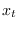 ,
,
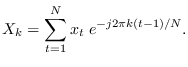 |
(10.5) |
Note that the circular power spectrum is the
expected value of the magnitude-squared DFT bins and is defined only at
the discrete DFT frequencies
Each stationary process can be approximated by a circularly stationary process whose circular power spectral
values are the same as the power spectrum values of the stationary process.
Unfortunately, if 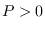 , the ACF of the stationary process
will be infinite in length because the output process has passed through
an infinite impulse response (IIR) filter.
So, the ACF, which is infinite, cannot be represented by the circular ACF.
However, as long as the ACF of the original process dies to zero prior to lag
, the ACF of the stationary process
will be infinite in length because the output process has passed through
an infinite impulse response (IIR) filter.
So, the ACF, which is infinite, cannot be represented by the circular ACF.
However, as long as the ACF of the original process dies to zero prior to lag 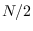 ,
the circular ACF will equal the original ACF over the first
,
the circular ACF will equal the original ACF over the first 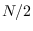 lags (See Figure 10.2).
By using circularly stationary processes as approximations
to stationary processes, we can obtain very efficient and tractable results
for PDF analysis and feature design.
lags (See Figure 10.2).
By using circularly stationary processes as approximations
to stationary processes, we can obtain very efficient and tractable results
for PDF analysis and feature design.
![]() that has a circular ACF, a circularly
stationary process, the circular power spectrum is also defined by
that has a circular ACF, a circularly
stationary process, the circular power spectrum is also defined by