Starting point
As we mentioned, we need to start MCMC-UMS with a valid  .
Inversion of the dimension-reducing transformation
.
Inversion of the dimension-reducing transformation
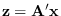 using pseudo-inverse
using pseudo-inverse
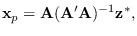 |
(5.11) |
produces a solution for  that meets the linear constraint
that meets the linear constraint
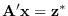 , but may have negative-valued elements.
A good initial starting point can be obtained from any
linear-programming solver. Specifically, we find
the solution to the maximization of
, but may have negative-valued elements.
A good initial starting point can be obtained from any
linear-programming solver. Specifically, we find
the solution to the maximization of
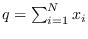 subject to
subject to
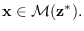 It makes no difference
if we are maximizing or minimizing since
It makes no difference
if we are maximizing or minimizing since 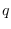 is fixed
anyway by the linear constraints. Any linear programming (LP)
algorithm such as OCTAVE glpk.m or MATLAB linprog.m
can output a “solution" which is a valid point.
See software/module_A_chisq_synth for additional details.
The best starting point, however, is the manifold centroid,
discused in Section 5.3.2.
is fixed
anyway by the linear constraints. Any linear programming (LP)
algorithm such as OCTAVE glpk.m or MATLAB linprog.m
can output a “solution" which is a valid point.
See software/module_A_chisq_synth for additional details.
The best starting point, however, is the manifold centroid,
discused in Section 5.3.2.