Algorithm description
The basic idea of MCMC-UMS is find one valid sample on the manifold,
then choose a direction to move along a 1-dimensional line
in the linear subspace spanned by the columns of matrix B.
If the manifold set is convex (it is in our case),
the valid points on the line are a compact interval,
the endpoints of which can be easily solved for, and
a new sample is chosen by uniformly sampling on the interval.
The process repeats by choosing a new direction, and repeating.
We consider two ways of choosing directions:
- the random-directions approach in which
a new random direction is chosen each time.
The random direction algorithm, also called
hit-and-run is suggested by Smith
[35,37,36].
The random direction is chosen by choosing a point
uniformly distributed on a hypersphere (by choosing a vector
of independent Gaussian random variables and normalizing
it to have length 1). Smith makes the claim in 2011 [35]:
“This version of hit-and-run
is considered to be the most efficient algorithm
for generating an asymptotic uniform point if the
set under consideration is convex".
- the systematic way of moving along the axes, by simply
changing each element of
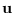 one at a time.
We see our systematic approach as a
simplification of slice sampling in multiple dimensions
[38], in which the target distribution is uniform.
Indeed, in slice sampling, the uniform samples
are drawn within an “axis-aligned" hyper-rectangle.
one at a time.
We see our systematic approach as a
simplification of slice sampling in multiple dimensions
[38], in which the target distribution is uniform.
Indeed, in slice sampling, the uniform samples
are drawn within an “axis-aligned" hyper-rectangle.
Here is a summary of the MCMC-UMS algorithm.
- As a starting point, we will need a vector
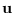 that is valid,
i.e. produces an
that is valid,
i.e. produces an  that lies in
that lies in
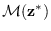 and
and
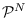 . Let
. Let 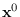 be a starting point,
then
be a starting point,
then
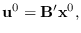 which maps back to
which maps back to 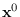 using (5.10).
using (5.10).
- We now seek a direction vector
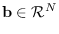 , of unit norm.
Clearly
, of unit norm.
Clearly 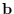 must lie in the column space of
must lie in the column space of 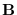 which span
the space in which we have freedom to move.
In the systematic method, we let
which span
the space in which we have freedom to move.
In the systematic method, we let 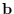 be a column of matrix
be a column of matrix 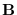 .
Each iteration, we choose the next column, in order,
returning back to the first column after
.
Each iteration, we choose the next column, in order,
returning back to the first column after 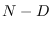 iterations.
In the random directions algorithm, we choose
iterations.
In the random directions algorithm, we choose 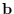 to be a random direction within the column space of
to be a random direction within the column space of 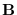 .
To do this, we generate an
.
To do this, we generate an 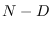 -dimensional vector
-dimensional vector 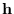 of independent standard normal variates, then normalize so that
of independent standard normal variates, then normalize so that
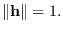 We then let
We then let
- We then create a new
 as follows:
as follows:
where  must lie in a compact interval of the real line
must lie in a compact interval of the real line
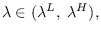 that includes
zero (to produce the current value
that includes
zero (to produce the current value 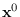 ).
We can easily find these limits as follows.
Define the vector
).
We can easily find these limits as follows.
Define the vector
![${\bf c} = [c_{1}, c_{2}, \ldots
c_{N}]$](img627.png) calculated from
calculated from 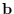 as
as
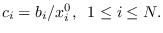 Then,
Then, 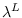 is -1 times the reciprocal of
the largest positive value of
is -1 times the reciprocal of
the largest positive value of 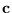 ,
and
,
and 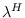 is -1 times the reciprocal of the most
negative value of
is -1 times the reciprocal of the most
negative value of 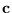 .
.
- We select
 by drawing a uniform
random variable in
by drawing a uniform
random variable in
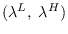 .
As long as
.
As long as  is sampled uniformly in this range,
the resulting (new) value of
is sampled uniformly in this range,
the resulting (new) value of  will be valid.
will be valid.
- We then set
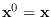 , and repeat (go to step 2).
, and repeat (go to step 2).
We can stop after a number of iterations
and let  be our generated sample of
be our generated sample of
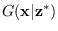 .
There is naturally a burn-in period required
to “forget" initial conditions.
.
There is naturally a burn-in period required
to “forget" initial conditions.