PDF form

Let ${\bf x}$ be the magnitude-squared of the DFT bins of a size-$N_t$ DFT. Then, $N=N_t/2+1$. Let ${\bf x}$ have mean $\bar{{\bf x}}$. Then, the distribution of the zero and Nyquist frequency bins ($i=1,N$) follows the Chi-squared distribution with 1 degree of freedom scaled by $\bar{x}_i$,

$$p(x_i) = \frac{1}{\bar{x}_i\sqrt{2\pi}}\; (x_i/\bar{x}_i)^{-1/2} \; \exp\left\{ -\frac{x_i}{2\bar{x}_i}\right\}, \;\; i=1, \;i=N.$$

DFT bins 1 through $N-1$ are complex so have the Chi-squared distribution with 2 degrees of freedom scaled by $\bar{x}_i/2$, or equivalently the exponential distribution with mean $\bar{x}_i$:

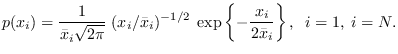
$$p(x_i) = \frac{1}{\bar{x}_i}\; \exp\left\{-\frac{x_i}{\bar{x}_i}\right\}, \;\; i\in [2,N-1].$$

The joint PDF of $p({\bf x};\bar{{\bf x}})$ is obtained from the product of the above bin densities. Interestingly, maximizing $p({\bf x};\bar{{\bf x}})$ over $\bar{{\bf x}}$ will also maximize the PDF of the input data to the DFT. Let ${\bf u}$ be the length-$N_t$ input to the DFT, then

$$\log p({\bf u}; \bar{{\bf x}}) = - \frac{1}{2} \sum_{i=1}^N \; \left\{ \log 2\pi \bar{x}_i + \frac{\vert U_i\vert^2}{\bar{x}_i} \right\},$$ (5.6)

where $U_i$ are the DFT bins. Therefore, we can replace $\vert U_i\vert^2$ with $x_i$:

$$\log p({\bf u}; \bar{{\bf x}}) = - \frac{1}{2} \sum_{i=1}^N \; \left\{ \log 2\pi \bar{x}_i + \frac{x_i}{\bar{x}_i} \right\},$$ (5.7)

It is mathematically simpler to maximize (5.7) instead of $p({\bf x};\bar{{\bf x}})$.

Although (5.7) is a function of $\bar{{\bf x}}$, we need to evaluate it for a particular value of the parameters ${\bf a}$ and $\sigma^2$. In Section 5.2.5, we showed how to compute $\bar{{\bf x}}$ from the AR parameters.