The Saddlepoint.

The $P\times 1$ saddlepoint vector $\lambda$ is the solution to the equation

$${\bf A}^\prime {\bf K}_u^1 = {\bf z},$$

where ${\bf K}_u^1$ is the diagonal matrix with diagonal element $i$ equal to $k_i/u_i$, written compactly (borrowing efficient MATLAB notation) as

$${\bf K}_u^1 = {\rm diag}({\bf k}./ {\bf u}),$$

where $u_i$ are the elements of vector ${\bf u}$ defined by

$${\bf u}= {\bf 1}-2{\bf A}$$$\lambda$$$,$$

where ${\bf 1}$ is a vector of 1's.

The saddlepoint approximation for $\log p({\bf z})$ is given by

$$l_{sp}=\frac{ -P\log(2\pi) - \log \det(2{\bf G}) -{\bf k}^\prime \log({\bf u}) -2 \mbox{\boldmath $\lambda$}^\prime {\bf z}}{2},$$

where $\log$ operates separately on each element and

$${\bf G}={\bf A}^\prime {\bf K}_u^2 {\bf A},$$

where

$${\bf K}_u^p = {\rm diag}({\bf k}./ {\bf u}^{\cdot p} ),$$

where ${\bf u}^{\cdot p}$ borrows the efficient MATLAB notation for element-wise exponentiation by $p$.

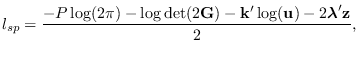
To find the saddlepoint, we initialize $\lambda$ to zeros, then implement the iterative Newton-Raphson search for the saddlepoint as described in [16]. For convenience, a MATLAB implementation is provided below in section 17.6.3.