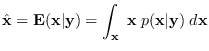Let the data vector 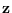 be composed of two parts
be composed of two parts
 and
and 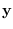 :
:
We have available training samples of 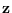 , however
in the future, only
, however
in the future, only 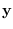 will be available
from which we would like to compute estimates of
will be available
from which we would like to compute estimates of  .
We will shortly see that the GM density facilitates
the computation of the conditional mean or
minimum mean square error (MMSE)
estimator of
.
We will shortly see that the GM density facilitates
the computation of the conditional mean or
minimum mean square error (MMSE)
estimator of  .
The conditional mean estimator is the expected value of
.
The conditional mean estimator is the expected value of  conditioned on
conditioned on 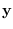 taking a specific (measured) value,
i.e.,
taking a specific (measured) value,
i.e.,
The maximum aposteriori (MAP) estimator is given by
Both the MAP and MMSE estimators are operations performed
on
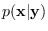 . Which estimator is most appropriate
depends on the problem.
Suffice it to say that the distribution
. Which estimator is most appropriate
depends on the problem.
Suffice it to say that the distribution
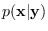 expresses all the knowledge we have about
expresses all the knowledge we have about  after
having measured
after
having measured 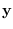 .
.
![$\displaystyle {\bf z}= \left[\begin{array}{cc} {\bf x} {\bf y}\end{array} \right].
$](img1521.png)