Next: Saddlepoint Approximation Up: M Quadratic and Linear Previous: M Quadratic and Linear Contents
The challenge is to determine the joint
PDF of ![]() under a specified Gaussian hypothesis, that is,
under a specified Gaussian hypothesis, that is,
Note that there is no loss of
generality in assuming that
![]() and
and
![]()
![]() ,
where
,
where ![]() is the
is the ![]() -by-
-by-![]() identity matrix
and
identity matrix
and
![]() is the
is the ![]() -by-1 vector of
zeros. Call this the white Gaussian noise (WGN) assumption
-by-1 vector of
zeros. Call this the white Gaussian noise (WGN) assumption ![]() . This is because we can write
. This is because we can write
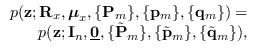
| (9.3) |
| (9.4) |