To solve (5.15), define
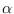 as the element-wise inverse of
as the element-wise inverse of
 .
Then, (5.15) can be written
.
Then, (5.15) can be written
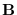
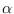
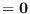 ,
which means that
,
which means that
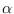 must be fully in the column space of
must be fully in the column space of 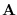 , or that
, or that
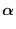 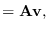 |
(5.17) |
for some 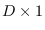 vector
vector 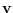 .
Therefore, to find the mean of the surrogate density,
we solve for the free variable
.
Therefore, to find the mean of the surrogate density,
we solve for the free variable 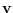 such that
such that
where
We can solve this by driving the square error to zero:
We can easily find derivative of
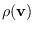 with respect
to
with respect
to 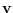 :
:
where
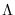
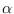
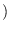 is the diagonal matrix with diagonal elements
is the diagonal matrix with diagonal elements
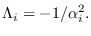 |
(5.22) |
We have found that if we use the negative-definite
Hessian approximation
![$\displaystyle \left[ \frac{\partial^2 \rho}{\partial v_k \partial v_l}\right]
\...
...A}^\prime {\mbox{\boldmath$\Lambda$}(\mbox{\boldmath$\alpha$})} {\bf A}\right),$](img678.png) |
(5.23) |
the resulting Newton-Raphson algorithm has excellent convergence properties
when starting with
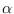
![$= [1, 1, \ldots 1]^\prime$](img679.png) .
Let
.
Let
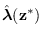 be the value of
be the value of
 at the solution to (5.18).
The algorithm to find
at the solution to (5.18).
The algorithm to find
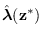 can be summarized as follows.
can be summarized as follows.
- Set iteration counter
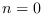 .
.
- To initialize, let
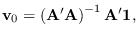 where
where 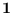 is the vector of ones.
is the vector of ones.
-
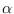
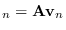 . Initially,
. Initially,
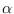 will be the
vector of ones.
will be the
vector of ones.
-

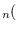
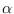
![$_n) = [1/\alpha_1, 1/\alpha_2, \ldots 1/\alpha_N]^\prime.$](img686.png)
- Compute derivative and Hessian according to (5.21),(5.22) and (5.23), then
update
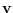 :
:
- Increment
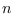 and go to step 3.
and go to step 3.
The algorithm is implemnted by software/lam_solve.m with dbound=0.
Although this method corresponds to classical
methods, it is based on a novel sampling argument
and can be extend to other manifolds as we will see.
![$\displaystyle {\bf v}_{n+1} = {\bf v}_n +
\left[ \frac{\partial^2 \rho}{\partial u_k \partial u_l}\right]^{-1}
\left[ \frac{\partial \rho}{\partial u_k}\right].$](img687.png)