Consider the feature stream
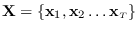 ,
where
,
where
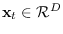 .
For simplicity, we assume that the first derivatives are obtained by the
first-order difference:
.
For simplicity, we assume that the first derivatives are obtained by the
first-order difference:
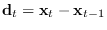 and define the DAF as
and define the DAF as
Note that we are forced to eliminate one time step, thus
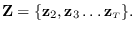 For analysis, it is more convenient to work with the equivalent history form of the DAF defined by
For analysis, it is more convenient to work with the equivalent history form of the DAF defined by
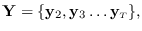 where
where
![$\displaystyle {\bf y}_t = \left[ \begin{array}{c} {\bf x}_{t-1} {\bf x}_{t} \end{array}\right].$](img1747.png) |
(15.1) |
From a theoretical point of view, features 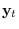 and
and 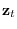 are equivalent
since we can obtain
are equivalent
since we can obtain 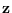 from
from 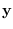 by linear transformation
by linear transformation
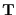 with determinant 1.
with determinant 1.
![$\displaystyle {\bf z}_t = \left[ \begin{array}{c} {\bf x}_t {\bf d}_{t} \end...
...t[ \begin{array}{c} {\bf x}_t {\bf x}_{t} - {\bf x}_{t-1} \end{array}\right].$](img1744.png)