PDF Modeling Introduction and Notation

The probability density function (PDF) of a random variable (RV) $X$ is defined by

$$p(x) \stackrel{\mbox{\tiny$\Delta$}}{=}\lim_{\delta \rightarrow 0} \; { {\rm Pr} \{ x-\delta/2 < X < x+\delta/2\} \over \delta}.$$

It is called a density function because it is the ratio of probability mass to differential area (or volume). Note that a particular value of $X$ is written in lower case $x$. The PDF $p(x)$ is regarded as a function of the particular value $x$. When a different RV is used, for example $p(z)$, the meaning of the function $p(\;)$ changes to that defined for the RV $Z$. When necessary, for example in the expression $p(T(x))$, we use a subscript. For example, when $z=T(x)$, we would write $p_z(T(x))$ to make it clear that $p(\;)$ is the PDF of RV $Z$. For multi-dimensional vectors written in bold notation, for example ${\bf x}\in {\cal R}^P$, the meaning of the density is extended to a density with respect to a differential volume in the $P$-dimensional space.

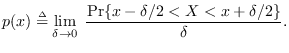
The simplest way to estimate the probability density of data is by histogram. A histogram is obtained by dividing the space of the RV into “bins", then counting the number of occurrences of the training data in each bin. A second step of smoothing or curve-fitting can be used to avoid the effects of random error. A method of PDF estimation that has become popular is that of Gaussian mixtures (GM). This can be regarded as the process of curve-fitting to a histogram where the curve is constrained to be a sum of positive Gaussian-shaped functions (modes or kernels), each with a different mean and variance. It also has the statistical interpretation of a mixture density - where each sample of the RV is regarded as having been a member of a sub-class corresponding to each mode. We will devote Section 13.2 to GM PDF estimation.

Multidimensional data, ${\bf x}\in R^P$, can be modeled by a multidimensional GM. However, when data consists of $K$ samples of dimension $P$, it is not necessary or even desirable to group all the data together into a single $K\times P$-dimensional sample. In the simplest case, all $K$ samples are independent and we may regard them as samples of the same RV. Normally, however, they are not independent. The Markovian principle assumes consecutive samples are statistically independent when conditioned on knowing the samples that preceded it. This leads to an elegant solution, the hidden Markov model (HMM), which employs a set of $M$ PDFs of dimension $P$. The HMM regards each of the $K$ samples as having originated from one of $M$ possible states and there is a distinct probability that the underlying model “jumps" from one state to another. We discuss the HMM, which uses GM to model each state PDFs, in section 13.3.

We discuss additional PDF models in the last section.