Alternative Parameterization

Consider the alternative MA parameters

$$\tilde{\mbox{\boldmath $\theta$}} = [ \tilde{b}_0, \tilde{b}_1, \ldots \tilde{b}_Q],$$

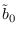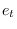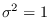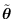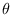where $\tilde{b}_0$ is not constrained to be 1 and we assume that $e_t$ has unit variance ( $\sigma^2=1$). We can relate the parameterization $\tilde{\mbox{\boldmath $\theta$}}$ to $\theta$ by a 1:1 transformation

$$\sigma^2=\tilde{b}_0^2, \;\; b_i = \tilde{b}_i/\tilde{b}_0, \; 1\leq i \leq Q.$$

The Fisher's information can be transformed using the matrix of derivatives

$${\bf H}_{ij} = \left[{\partial \theta_i \over \partial \tilde{\th... ...0 \\ -\tilde{b}_3/\tilde{b}_0^2 & 0 & 0 & 1/\tilde{b}_0 \end{array}\right]$$

We have that

$$\left[ \frac{ \partial \log p({\bf x}) } { \partial \tilde{\theta... ...\bf H}\; \left[ \frac{ \partial \log p({\bf x}) } { \partial \theta } \right],$$

and

$${\bf I}_{\tilde{\mbox{\boldmath $\theta$}}} = {\bf H}^\prime \; {\bf I}_{\mbox{\boldmath $\theta$}} \; {\bf H}.$$