Illustration of PDF Projection
PDF projection is illustrated in Figure
2.1.
In the figure, we see a feature transformation
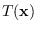 that maps the high-dimensional data space
that maps the high-dimensional data space
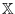 into a lower-dimensional feature
space
into a lower-dimensional feature
space
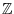 . A reference distribution
. A reference distribution
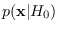 is shown in the input data space
is shown in the input data space
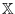 and feature
space
and feature
space
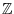 , where it is written
, where it is written
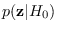 .
A feature distribution
.
A feature distribution
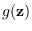 is also shown.
On the basis of knowing
is also shown.
On the basis of knowing
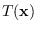 ,
,
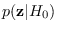 ,
,
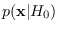 , and
, and
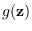 ,
we construct the density
,
we construct the density
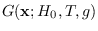 ,
using formula (2.2) which
is shown in the figure. We say that
,
using formula (2.2) which
is shown in the figure. We say that
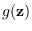 has been projected to the input data space.
Because
has been projected to the input data space.
Because
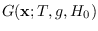 is a member of the
class of distributions on
is a member of the
class of distributions on
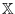 that
generate feature distribution
that
generate feature distribution
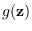 through transformation
through transformation
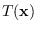 , it is an estimate
of a distribution of
, it is an estimate
of a distribution of  that could have
generated
that could have
generated
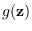 .
If
.
If
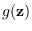 is an estimate of the
feature distribution, then
is an estimate of the
feature distribution, then
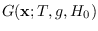 can be seen as an estimate of the input data distribution
can be seen as an estimate of the input data distribution
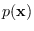 .
.
Also seen in the figure is the level set
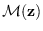 , which is the set
of all points
, which is the set
of all points  that map to a given point
that map to a given point  in the feature space.
To draw a sample from
in the feature space.
To draw a sample from
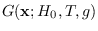 , we first draw a sample
, we first draw a sample
 from
from
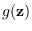 , then draw a sample from set
, then draw a sample from set
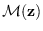 .
The sample is drawn from
.
The sample is drawn from
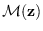 , not uniformly, but
proportional to
, not uniformly, but
proportional to
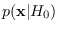 .
.
In Chapter 3, we will discuss maximum entropy PDF projection
in which we choose 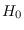 to produce the distribution that has maximum entropy
among all possible PDFs consistent with
to produce the distribution that has maximum entropy
among all possible PDFs consistent with
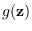 . But for now, assume that
. But for now, assume that 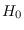 is user-selected.
is user-selected.
Figure 2.1:
Illustration of PDF projection.
|
|
![]() , which is the set
of all points
, which is the set
of all points ![]() that map to a given point
that map to a given point ![]() in the feature space.
To draw a sample from
in the feature space.
To draw a sample from
![]() , we first draw a sample
, we first draw a sample
![]() from
from
![]() , then draw a sample from set
, then draw a sample from set
![]() .
The sample is drawn from
.
The sample is drawn from
![]() , not uniformly, but
proportional to
, not uniformly, but
proportional to
![]() .
.
![]() to produce the distribution that has maximum entropy
among all possible PDFs consistent with
to produce the distribution that has maximum entropy
among all possible PDFs consistent with
![]() . But for now, assume that
. But for now, assume that ![]() is user-selected.
is user-selected.